I read first chapters of your textbook, and now I can discuss your question.
First of all, there are too few words in your solution, and it is difficult (in fact, impossible) to understand anything. For example,
Пусть
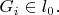
what
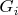
means here ? Is this an open set in topology

? If so, what is the role of the subscript

?
Next,
Возьмем
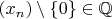
What is the meaning of this formula at all ?

usually means a sequence,
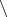
the sign of set difference,

a set (of a single element

), but how can we subtract a set from a sequence ? And difference of two sets is a set, not a rational number, so we can not write "
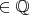
" ... Probably you should try to write in a more classical style, not in a short manner like in "Expansion" sections of McCluskey.