В учебнике по линейной алгебре, который я читаю, есть такой задание:
Цитата:
Для того, чтобы доказать это утверждение, я составил таблицу вариантов значений

при которых

и искал хотя бы одно не тривиальное решение для каждого из вариантов (Обозначения:

- значение равно нулю,

- значение не равно нулю,

- значения соответствующих компонентов вектора

при которых

становиться равным нулю, первая строка заголовок таблицы):
Цитата:
Потом я полез в ответы, чтобы сравнить решения и увидел у автора такой ответ:
Цитата:
a) Suppose

and

. If
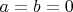
, then examine

. This has the solution

. This solution is nonzero, except when

. In that case, however,

is the zero matrix, and

for every vector

.
b) Finally, if

and

are not both zero, set

. Then

, because

. Thus,

is a nontrivial solution of

. So, in all cases, the equation

has more than one solution.
Мне не понятно по какой логике часть a) доказательства автора доказывает все варианты описанные в первых 9-ти строках моей таблицы?