Строго можно было бы рассуждать так. Рассмотрим сечение конуса плоскостью

, проходящей через его ось

и через точку

. Эта плоскость пересекает конус по двум лучам

и

. Она содержит прямые

и

(диагонали верхнего и нижнего квадратов). Эти прямые параллельны, значит треугольники

и

подобны. (Здесь

есть точка пересечения отрезка

и луча

). Но

,

(где

--- высота конуса),

(радиус нижней окружности),

(радиус верхней окружности). Отсюда имеем соотношение

, и в итоге находим

.
Дальше надо найти угол между плоскостями

, т.е. плоскостью нижнего основания параллелепипеда, и плоскостью

. С этой целью сначала надо понять, по какой прямой плоскость

пересекает плоскость нижнего основания. Пусть

--- точка пересечения прямой

и плоскости

. Ясно, что она лежит на прямой, которая является проекцией прямой

на плоскость

. Проекция точки

на

есть

, проекция

есть

, значит проекция прямой

--- это прямая

, т.е.

, вторая диагональ нижнего квадрата. Затем, из подобных треугольников
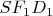
и

находим

, откуда

. Короче,

--- это точка, лежащая на диагонали

на расстоянии

от

. Ну, а искомая прямая --- это как раз

.
Теперь, значит, имеем такую ситуацию. Из точки

исходят три луча

,

и

, и они, заметим, попарно перпендикулярны. А точки

,

,

лежат на этих лучах на расстоянии

,

и

от

, соответственно. И нам надо найти угол между плоскостями

и

.
Легко решить и более общую задачу: пусть

,

,

--- три попарно перпендикулярных луча,

,

,

. Каков угол между плоскостями

и

? Пусть
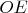
--- высота в треугольнике

, опущенная на гипотенузу

. Легко понять, что плоскость

перпендикулярна

, т.е. линии пересечения плоскостей

и

, и угол между последними плоскостями равен углу

в треугольнике

(по определению того, что такое двугранный угол). Учитывая, что угол

в треугольнике

--- прямой, видим, что тангенс угла

есть

, т.е. искомый угол между плоскостями --- это

. Легко видеть, что в прямоугольном треугольнике с катетами

и

высота, опущенная на гипотенузу, есть

. Отсюда

, значит искомый угол между плоскостями --- это

.
Применяя этот общий факт в нашем случае, и производя вычисления, видим, что ответ есть

, как выше и написано.
.



