Для демонстрации применимости работы [1] численно было выполнено в Maple 15 интегрирование уравнения

с начальным условием

[Так как Maple находит решение краевой задачи, для численного интегрирования задавались условия

,

. Значение 50 было подобрано из соображений, чтобы граничные условия практически не оказывали влияния на решение.]
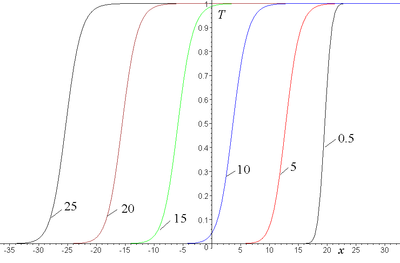
На рис. построены профили решения в моменты времени подписанные над кривыми (через одинаковые промежутки времени за исключением первого профиля).
Вложение:
 KPP.PNG [ 21.58 Кб | Просмотров: 0 ]
KPP.PNG [ 21.58 Кб | Просмотров: 0 ]
Как и следует из теории, после непродолжительного переходного периода решение приобретает форму бегущей волны. (На рис. показан один из переходных профилей в момент времени 0.5). Далее за время 5 профили сдвигаются на величину 10. Следовательно (как и вытекает из теории КПП) скорость равна 2.
Ref
1. Колмогоров А.Н., Петровский И.Г., Пискунов Н.С. Исследование уравнения диффузии, соединённой с возрастанием кол-ва вещества и его применение к одной биологической проблеме // Бюл. МГУ Математика и механика, 1937 — Т.1., вып. 6. — с 1–26. [Эта работа включена в книгу: Колмогоров А.Н. Избр. тр. Математика и механика. — М.: Наука, 1985].



