Выглядит привлекательной идея вести перебор по

. В этом случае наиболее затратной операцией является факторизация

.
С другой стороны, мы ищем только такую факторизацию

, у которой

делится на

(точнее, конечная цель — чтобы оно делилось на

). То есть, если

, то должно быть

. Далее, поскольку

, нас устраивает только такой остаток

, для которого

является квадратичным вычетом по тому же модулю

.
На конкретном примере:

. Мы должны искать такие сомножители

, что остатки от деления

и

на

противоположны (пусть будут

и
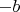
) и

(точнее, в задаче нам нужно

, но мы пока ищем там, где светлее). Для

таких

всего четыре:

,

,

,

. Т.е. мы должны искать сомножители

и

, которые имеют только эти 4 остатка при делении на

. В данном примере действительно, есть такое разложение:

. Видно что сомножители имеют при делении на

противоположные остатки

, поэтому их сумма делится на

(и даже на

, но не на

, как нам надо). Могут ли эти соображения как-то радикально сократить время факторизации, да и можно ли вообще быстро отыскать нужные квадратичные вычеты — для меня тёмный лес.
-- Вс мар 17, 2024 14:37:50 --Можно показать, что остаток от деления

на

равен 4 либо 13. Это, конечно, даёт сокращение перебора на порядок, но такое сокращение я не назову радикальным.



