Всё-таки чуть более конкретно поясню, откуда появляется вопрос.
Уравнения Янга-Миллса

можно записать в виде недоопределённой эволюционной системы со связью. Для этого

будем воспринимать как полноправные зависимые координаты, а

лишь как обозначение для

Теперь уравнения Янга-Миллса можно записать в искомом виде

Первое уравнение просто определяет

в терминах

, третье получается при
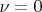
, второе при

.
Последнее уравнение (оно же связь) и приводит к исходному вопросу, где

, а из исходной формы связности

удалено связанное со временем слагаемое

. Геометрически это всё лишь причуды того куда и как вложили систему, но для счёта внутри уравнений (бесконечно продолженных, т.е. вместе со всеми дифференциальными следствиями) приходится с этим соотношением разбираться.
Надеюсь, я не наврал со всеми этими индексами...