Нет, доказательства из статьи я не понял, соответствующую алгебру не знаю. Зато придумал сам простое "школьное" доказательство - что и хотел. Причём опять по той же схеме, что ранее я писал для
![$Q(\sqrt{x}, \sqrt[3]{x})$ $Q(\sqrt{x}, \sqrt[3]{x})$](https://dxdy-01.korotkov.co.uk/f/c/d/c/cdce209fec5e92e6b213197095d55f5b82.png)
. Только вместо

будут

, где

.
Если есть поле

и

, обозначим

. При

нужно понять структуру расширения

, назовём это трисекторным расширением. При

это будет

. Используя

и школьные формулы косинуса двойного угла, суммы косинусов, косинуса суммы, несложно выразить

в виде линейной комбинации

с коэффициентами из

. Обратный элемент к данному можно найти, просто решив систему линейных уравнений относительно его коэффициентов, которая получается из того, что при умножении на данный должна быть

.
Далее при тех же условиях из

вытекает (т.к. косинус двойного угла выражается через квадрат одинарного), что представление выше единственно в том смысле, что если

, то и

.
Итак, теорема: Если кубическое уравнение с рациональными коэффициентами и отрицательным дискриминантом не имеет рациональных корней, то его действительный корень не может принадлежать

.
Предположим противное. Пусть существуют кубические уравнения с рациональными коэффициентами и отрицательным дискриминантом, без рациональных корней и у каждого есть корень, принадлежащий

. Тогда этот корень принадлежит цепочке квадратичных или трисекторных расширений полей:

, где

или

для этих

и

. Выберем среди всех этих уравнений и цепочек полей такие, у которых число трисекторных образующих в составном расширении для этого корня минимально по сравнению с другими, а среди них те, у которых число квадратичных образующих минимально. Т.е. если взять любое такое уравнение и его корень из

, то у него число трисекторных образующих не меньше, а при равном числе трисекторных образующих число квадратичных (или, что то же, всех) образующих не меньше. Обозначим суммарное число образующих корня выбранного уравнения через

.
Таким образом, есть кубическое уравнение с отрицательным дискриминантом без рациональных корней

действительный корень которого будет числом, принадлежащим

. Обозначим этот корень через
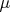
. Он получается из цепочки полей

, где

или

для этих

и

. Отметим, что для трисекторного расширения

не только

, но и

, поскольку при

мы бы это трисекторное расширение могли бы заменить квадратичным (т.е. заменить эту трисекцию построением циркулем и линейкой) и получили бы противоречие с тем, что у нас минимальное количество трисекторных расширений.
В зависимости от степени последнего расширения возможны два случая:

или

.
В первом случае существуют такие

, что

, причём

. Дальнейшее рассуждение тогда дословно повторяет доказательство теоремы 2.18 в Martin, Geometric Constructions: подставим

в уравнение, увидим, что если

- корень, то и

- тоже корень и они разные, а тогда по теореме Виета третий корень выражается как

минус сумма этих и принадлежит

- получаем противоречие с тем, что

- минимальное.
Во втором случае существуют такие

, что

, где через

обозначено

, причём

или

и

. Рассмотрим величины, полученные сдвигами

в выражении
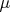
на

:

Подставим их в наше кубическое уравнение. Поскольку, как было написано выше,

представляются линейными комбинациями

с коэффициентами из

, то вообще любые натуральные степени и их произведения величин

представляются такими линейными комбинациями. Более того, поскольку и для сдвинутых углов

, то раскрыв все скобки и собрав линейные комбинации после подстановки в кубическое уравнения, получим, что его правая часть равна

Ну а теперь при

у нас

корень, значит, выражение выше равно

. Но тогда

. Но тогда раскрыв по косинусу суммы в этом выражении, видим, что и

- тоже корни. Итак, мы нашли три несовпадающих (это можно показать, если их приравнять и раскрыть по сумме косинусов, получим

) действительных корня, что противоречит тому, что у уравнения отрицательный дискриминант - тогда должен быть только один действительный корень.



