Knight2023
Это не беда, возьмите какое-то еще покрытие. Проверьте, а не будет ли сумма меньше.
И еще какое-то. И еще раз проверьте.
Вам нужно найти инфимум по всем покрытиям. А пока мы нашли только одно. Ясно, что инфимум может быть меньше.
Considering the same partition that we had:
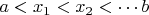
, we can develop a cover like this one:
![$$
\lbrace
(0,a], (a, x_1], (x_1, x_2], \cdots, (x_{n-1}, b]
\rbrace
$$ $$
\lbrace
(0,a], (a, x_1], (x_1, x_2], \cdots, (x_{n-1}, b]
\rbrace
$$](https://dxdy-02.korotkov.co.uk/f/9/f/2/9f242c7beba1f097832f7fa67373971682.png)
And we can write the measure as:
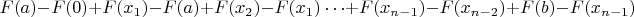
That is a telescopic sum, which results into
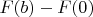
, and if we define
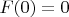
, the measure of that cover (I mean the measure of the union of the elements of that cover) is
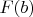
.
-- 12.12.2023, 17:47 --I guess, I can do a little better:
Take a very small

, and for the same partition we have the following cover:
![$$
\lbrace
(a- \delta, a],
(a, x_1],
\cdots,
(x_{n-1}, b]
$$ $$
\lbrace
(a- \delta, a],
(a, x_1],
\cdots,
(x_{n-1}, b]
$$](https://dxdy-01.korotkov.co.uk/f/8/5/f/85f343f124e1a23003a224cfaa17650982.png)
And taking the measure would result into telescopic sum, leaving us with
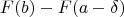
As

can be made as small as we please, we have the infimum
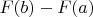
and it well corresponds with the notion of length of an interval.