Магнитное поле как релятивистское следствие электрического.

[svv]

Рассмотрим силы, которые действуют на второй провод со стороны первого.

В лабораторной СО (в которой неподвижны ионы) провода нейтральны. Поэтому суммарная сила, действующая на любой ион второго провода со стороны электронов и ионов первого провода, равна нулю (электрическое поле равно нулю по причине нейтральности, а магнитное на неподвижный ион не действует). Значит, эта сила равна нулю и в СО электронов.
Сила, действующая на электрон второго провода в СО электронов, складывается из силы со стороны электронов первого провода и силы со стороны ионов первого провода. Но плотность электронов в их собственной системе меньше, чем в лабораторной, а плотность ионов в той же системе — больше, чем в лабораторной. Значит, сила притяжения больше, чем сила отталкивания.
____________________________

Теперь вместо второго провода возьмём один заряд $q$, неподвижный в лабораторной СО. Сумма сил, действующих на него со стороны первого провода, равна нулю (опять, потому что в лабораторной системе электрическое поле провода равно нулю в силу его нейтральности, а магнитное не действует на неподвижный заряд). Значит, сила, действующая на заряд, будет нулевой и в СО электронов.

Пусть в лабораторной СО линейные плотности заряда ионов и электронов провода равны соответственно $+\sigma$ и $-\sigma$, а скорость электронов равна $\mathbf v$. Тогда в СО электронов линейные плотности заряда ионов и электронов будут соответственно $\gamma\sigma$ и $-\gamma^{-1}\sigma$, где $\gamma=\frac 1{\sqrt{1-\frac{v^2}{c^2}}}$.
Если плотности разные, почему равнодействующая равна нулю? Потому что в СО электронов заряд движется со скоростью $-\mathbf v$, и на него, помимо электрического, действует и магнитное поле (со стороны ионов провода, также движущихся со скоростью $-\mathbf v$). Отсюда легко вывести, чему равна магнитная составляющая силы Лоренца.

(Оффтоп)

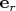
В СО электронов. Расстояние от провода до заряда равно $r$. В точке, где находится заряд, построим единичный вектор $\mathbf e_r$ перпендикулярно проводу (направим от провода). Электрическое поле
$\mathbf E=\dfrac {2(\gamma-\gamma^{-1})\sigma}r\mathbf e_r$
Электрическая сила, действующей на заряд:
$\mathbf F_e=\dfrac {2q(\gamma-\gamma^{-1})\sigma}r\mathbf e_r=\dfrac {2q\gamma(1-(1-\frac{v^2}{c^2}))\sigma}r\mathbf e_r = q\dfrac{v}{c}\dfrac {2\gamma\sigma v}{cr}\mathbf e_r$
Магнитная сила — противоположный вектор (чтобы равнодействующая была нулевой):
$\mathbf F_m=-q\dfrac{v}{c}\dfrac {2\gamma\sigma v}{cr}\mathbf e_r=q\dfrac{v}{c}\dfrac {2I}{cr}\mathbf e_r,$
где $I=\gamma\sigma(-v)$ — сила тока, обусловленная движением ионов "назад". То же получится из выражения для магнитной силы Лоренца, если подставить магнитное поле провода и взять скорость заряда $(-\mathbf v)$, параллельную проводу.

[Orion_123]

svv в сообщении #1620309 писал(а):

Рассмотрим силы, которые действуют на второй провод со стороны первого.

Но плотность электронов в их собственной системе меньше, чем в лабораторной, а плотность ионов в той же системе — больше, чем в лабораторной. Значит, сила притяжения больше, чем сила отталкивания.

Вы не учитываете отталкивание электронов одного провода от электронов другого. Т.к. в неподвижной со плотность обоих выше, значит сила отталкивания выше квадратично. И она должна пересилить притягивание.



Допустим, скорость электронов такая, что их плотность повышается в два раза. Рассмотрим "срез" проводов, в котором один ион и два электрона. Посчитаем силы:

1) Отталкивание между ионами = 1
2) Отталкивание между электронами = 4
3) Притягивание между электронами одного провода и ионами второго = 4

Суммарная сила = 1 отталкивание. А должно быть притягивание. Где ошибка?

[Dedekind]

Orion_123
Вам же уже не один раз сказали - ошибка в том, что в лабораторной СО плотность электронов равна плотность ионов. Вы разобрались с парадоксом Белла?

[Orion_123]

Dedekind в сообщении #1620334 писал(а):

Orion_123
Вам же уже не один раз сказали - ошибка в том, что в лабораторной СО плотность электронов равна плотность ионов. Вы разобрались с парадоксом Белла?

Если плотности одинаковы, то откуда тогда сила притяжения или отталкивания?

Как применить парадокс Белла к этой ситуации - мне не понятно.

[sergey zhukov]

Orion_123
В общем, все уже нужное уже было сказано. И очень даже понятно. И даже вычислено. Перечитывайте. Уверяю вас, что svv все учитывает, а вот вы - нет.

[DimaM]

Orion_123 в сообщении #1620335 писал(а):

Если плотности одинаковы, то откуда тогда сила притяжения или отталкивания?

Из-за магнитного поля. Это в ЛСО.
В СО электронов будет повышенная плотность движущихся ионов, что даст, помимо электростатического, еще их магнитное взаимодействие.

[Orion_123]

svv в сообщении #1620309 писал(а):

Рассмотрим силы, которые действуют на второй провод со стороны первого.

Но плотность электронов в их собственной системе меньше, чем в лабораторной, а плотность ионов в той же системе — больше, чем в лабораторной. Значит, сила притяжения больше, чем сила отталкивания.

В системе отсчета электронов мне тоже непонятно откуда сила притяжения. Допустим, ток настолько большой, что в СО электронов плотность электронов будет близка к нулю, а плотность ионов очень высокая. В таком случае очевидно, что ионы будут сильно отталкиваться, а притяжение будет принебрежимо мало.

[Dedekind]

Orion_123 в сообщении #1620335 писал(а):

Как применить парадокс Белла к этой ситуации - мне не понятно.

Корабли - электроны. Разгон кораблей - включение источника питания.

Orion_123 в сообщении #1620335 писал(а):

Если плотности одинаковы, то откуда тогда сила притяжения или отталкивания?

Вы знаете, что такое магнитное поле и сила Лоренца?

[Orion_123]

Dedekind в сообщении #1620349 писал(а):

Корабли - электроны. Разгон кораблей - включение источника питания.

Это мне понятно, оно объясняет почему в неподвижной СО нет увеличения плотности электронов. Но это не объясняет откуда в этой ситуации сила притяжения (а она должна быть видна в неподвижной СО)

Dedekind в сообщении #1620349 писал(а):

Вы знаете, что такое магнитное поле и сила Лоренца?

Но ведь топик о том, как объяснить силу без привлечения классической электродинамики, только средставми силы Кулона и релятивизма.

[Dedekind]

Orion_123 в сообщении #1620350 писал(а):

Это мне понятно, оно объясняет почему в неподвижной СО нет увеличения плотности электронов. Но это не объясняет откуда в этой ситуации сила притяжения

От силы Лоренца.

Orion_123 в сообщении #1620350 писал(а):

Но ведь топик о том, как объяснить силу без привлечения классической электродинамики, только средставми силы Кулона и релятивизма.

Для двух проводов это невозможно. Просто потому, что в ЛЮБОЙ ИСО и в одном проводе, и в другом, будут движущиеся заряды. Так что это не лучший пример. Вот для одного провода и летящего параллельно электрона - тут да, можно обойтись без магнитной силы (в ИСО электрона). Но даже там магнитное поле все равно будет присутствовать.

[Orion_123]

Dedekind в сообщении #1620352 писал(а):

Для двух проводов это невозможно. Просто потому, что в ЛЮБОЙ ИСО и в одном проводе, и в другом, будут движущиеся заряды. Так что это не лучший пример. Вот для одного провода и летящего параллельно электрона - тут да, можно обойтись без магнитной силы (в ИСО электрона). Но даже там магнитное поле все равно будет присутствовать.

Т.е. магнитное поле не является релятивистским следствием электрического?

[Dedekind]

Orion_123 в сообщении #1620354 писал(а):

Т.е. магнитное поле не является релятивистским следствием электрического?

Смотря какой смысл вкладывать в эти слова. Существует единое электромагнитное поле. У него есть компоненты: электрическое и магнитное. Эти компоненты связаны между собой некоторыми хитрыми законами (уравнениями Максвелла). В различных СО эти компоненты преобразуются по определенным правилам (например, см. тут, уравнения 6.38 https://online.mephi.ru/courses/physics ... 6/6.7.html ). В некоторых ситуациях можно подобрать такую СО, что либо электрическое поле, либо магнитное поле будут равняться нулю. Но не всегда и не для любой системы зарядов.

Кроме того, отдельно существует сила Лоренца, которая действует на заряженные частицы со стороны этих полей. Для любой частицы, движущейся с любой скоростью, магнитную силу Лоренца на нее можно занулить, перейдя в СО этой частицы. Но это не гарантирует того, что в этой СО магнитное поле и магнитная сила также исчезнут для всех остальных частиц. Что и демонстрирует пример с двумя проводами.

Об остальном Вам расскажут более прошаренные в физике участники, чем я:)

[sergey zhukov]

Orion_123
Тут нужно прежде всего вот что понимать. Допустим, вы сидите в лодке, которая плавает в океане. Мимо проплыл океанский лайнер и поднял волну. Волна дошла до вас и вы закачались на волнах. С чем взаимодействует ваша лодка? С лайнером? Нет, только с водой. Лайнер создал волны, и теперь он может делать что угодно. Может уплыть, остановиться или вообще утонуть. Отныне волны существуют самостоятельно и вы имеете дело только с ними. Когда волны дошли до вас, вам вообще нет дела до того, что там делает сейчас лайнер. Вы смотрите только на то, насколько сильные волны находятся прямо под вашей лодкой.

Электромагнитное поле - это именно такие волны. Заряды и токи создают его, но дальше оно живет само. Это просто еще один участник взаимодействий. В океане есть лайнер, лодка и вода, а в электродинамике - какие-то внешние токи и заряды, ваш пробный заряд и электромагнитное поле.

Наш пробный заряд (тот, движение которого мы хотим найти) совершенно "слепой". Он не знает и не видит ничего, что не было бы прямо в той точке, где он находится. Т.е. он знает и видит только электромагнитное поле в крошечной области вокруг себя. На самом деле это все, что ему нужно знать, чтобы "правильно" двигаться. Ему нет дела, как далеко от него и в каком направлении находятся токи и заряды, какие они и как меняются. Он имеет дело только с кусочком электромагнитного поля вокруг себя и больше ни с чем. Электромагнитное поле - это такой же реальный объект, как вода в океане. У этого поля есть энергия и импульс (но нет массы).

Тела по разному выглядят в разных СО. Скажем, сокращаются в продольном направлении. Электромагнитное поле тоже выглядит по разному в разных СО. Можно сказать, что оно тоже как-то "сокращается" (на самом деле преобразуется). Только электромагнитному полю в целом можно приписать такую самостоятельность, сделать его почти таким же объектом, как материальное тело.

Да, в СО пробного заряда всегда оказывается, что действует на него только электрическое поле. Но чтобы это электрическое поле в этой СО пробного заряда вычислить, очень полезно использовать цельную сущность "электромагнитное поле", с которой и только с которой в точке своего нахождения взаимодействует заряд. Преобразовав электромагнитное поле в СО заряда, мы получаем электрическое поле, которое и действует на заряд. Действует на заряд только электрическое поле, но получается оно путем преобразования электромагнитного поля в СО заряда. Само по себе электрическое поле не является таким самостоятельным объектом, как электромагнитное.

Т.е. знание только одного электрического поля в точке не позволяет нам вычислить, как будет выглядеть это же поле в СО заряда, который движется в этой точке. Нам потребуется преобразовать согласно преобразованиям Лоренца всю конфигурацию зарядов и токов вокруг этой точки, чтобы вычислить электрическое поле в СО заряда. Скажем нам придется думать о том, как "сжимаются провода", "повышается линейная плотность заряда", "электроны того другого тока в этой СО имеют другую скорость" и пр. Но все это не нужно, если к электрическому полю в точке добавить еще и магнитное, т.е. рассматривать самостоятельную сущность - электромагнитное поле. Тогда нам нужно преобразовывать только это поле в точке, а думать о том, что там и где сжимается и повышается, вообще не нужно. Все это уже учитывается магнитной составляющей только в этой точке. Точнее, это следует из того, что заряд взаимодействует только с электромагнитным полем, а значит ему все равно, что происходит на некотором отдалении. Это очень удобно.