RIPВ общем, вот моё доказательство теоремы Кима (а значит — и решение исходной задачи). Можете оценить, сравнить с известными Вам? Мне лично больно читать статью Кима (хотя есть вероятность, что там всё элементарно и я чего-то не понимаю) — а сам я использую только теорему Дирихле и простой факт из теории меры.
(Решение)
Пусть

— иррациональное число.
Теорема Кима. Для почти всех
![$s \in \mathbb[0; 1]$ $s \in \mathbb[0; 1]$](https://dxdy-03.korotkov.co.uk/f/2/7/7/277cdcf2cbf9749277fcc5695c5f614e82.png)
выполняется

.
Если

не принимает нулевых значений, то

равносильно тому, что

принимает сколь угодно малые значения. Избавляясь от множества меры 0

, получим ещё одну формулировку теоремы.
Снова теорема Кима. Для почти всех
![$s \in [0;1]$ $s \in [0;1]$](https://dxdy-03.korotkov.co.uk/f/2/6/c/26c4bd8fb9cd18a38d893b0b41da37a882.png)
и для всякого

найдётся

с

.
Пользуясь тем, что пересечение (по всем

) счётного набора множеств меры

есть множество меры

, теорему Кима можно получить из следующего утверждения.
Ещё раз теорема Кима. Для всякого

для почти всех
![$s \in [0; 1]$ $s \in [0; 1]$](https://dxdy-01.korotkov.co.uk/f/8/0/d/80d3fd4c633c5eb6a315f05d23dac97382.png)
найдётся

c

.
Теперь для красоты заменим
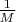
на

, а последнее условие — на
![$s \in [n\theta - \frac{\varepsilon}{n}; n\theta + \frac{\varepsilon}{n}] + \mathbb{Z}$ $s \in [n\theta - \frac{\varepsilon}{n}; n\theta + \frac{\varepsilon}{n}] + \mathbb{Z}$](https://dxdy-02.korotkov.co.uk/f/1/b/e/1befff18920219fadb54df5fa7bfd70282.png)
.
Кима. Пусть
![$A_n = [n\theta - \frac{\varepsilon}{n}; n\theta + \frac{\varepsilon}{n}] + \mathbb{Z}$ $A_n = [n\theta - \frac{\varepsilon}{n}; n\theta + \frac{\varepsilon}{n}] + \mathbb{Z}$](https://dxdy-02.korotkov.co.uk/f/9/3/d/93dd8a8cc5852bcaec739adb7f0abfbe82.png)
. Тогда
![$A = \bigcup_{n = 1}^{+\infty} \left(A_n \cap [0;1]\right)$ $A = \bigcup_{n = 1}^{+\infty} \left(A_n \cap [0;1]\right)$](https://dxdy-04.korotkov.co.uk/f/b/2/0/b207415978b03a6527bc799d04bb9f6f82.png)
имеет меру 1.
(очевидно,

измеримо)
Доказательство теоремы Кима. Далее все отрезки рассматриваем

, то есть записывая
![$[a;b]$ $[a;b]$](https://dxdy-04.korotkov.co.uk/f/f/5/f/f5ff45e36cee967b17a810445d436aaa82.png)
имеем в виду
![$([a;b] + \mathbb{Z}) \cap [0;1]$ $([a;b] + \mathbb{Z}) \cap [0;1]$](https://dxdy-04.korotkov.co.uk/f/3/7/f/37f4bd65a820f02adb0d843f694403e482.png)
.
Пусть

и

такие, что

(таких

существует сколь угодно много по теореме Дирихле, причём тогда

и

взаимно просты). Пусть

— рациональное число со знаменателем

. Пусть

такое, что

. Тогда

, то есть
![$e \theta \in [\frac{m-1}{N}; \frac{m+1}{N}] = B_{m,N}$ $e \theta \in [\frac{m-1}{N}; \frac{m+1}{N}] = B_{m,N}$](https://dxdy-01.korotkov.co.uk/f/4/b/c/4bc558c11a0e9f1ecf8a018a19e27c3582.png)
. Если
![$e \theta \in [\frac{m-1}{N}; \frac{m}{N}]$ $e \theta \in [\frac{m-1}{N}; \frac{m}{N}]$](https://dxdy-04.korotkov.co.uk/f/3/d/2/3d255ff5f90dce47da2b2bdec572612a82.png)
, то множество
![$[e\theta; e \theta + \frac{\varepsilon}{N}]$ $[e\theta; e \theta + \frac{\varepsilon}{N}]$](https://dxdy-03.korotkov.co.uk/f/e/4/8/e486eabede740655c02a7ae72b459c0e82.png)
содержится как в

(поскольку

), так и в

(поскольку

), и получаем

. Аналогично рассматривается случай
![$e\theta \in [\frac{m}{N}; \frac{m+1}{N}]$ $e\theta \in [\frac{m}{N}; \frac{m+1}{N}]$](https://dxdy-04.korotkov.co.uk/f/b/7/a/b7aac3d15c4269eb607593c7584924d482.png)
.
Остался один шаг: воспользоваться утверждением ниже, взяв в качестве класса

всевозможные

,

и

.
Упражнение по теории меры. Пусть
![$A \subset [0;1]$ $A \subset [0;1]$](https://dxdy-02.korotkov.co.uk/f/d/c/8/dc89ab09b8f25966a24f8f1f016b00d782.png)
— произвольное измеримое множество, а

— класс множеств такой
(обычно это класс всех отрезков), что для всякого измеримого
![$B \subset [0;1]$ $B \subset [0;1]$](https://dxdy-01.korotkov.co.uk/f/c/3/a/c3a9a5a9b3194fe270f9507254abd34982.png)
и

найдутся

такие, что их попарные пересечения имеют меру

, и

. Пусть найдётся

такое, что для всех

выполняется

. Тогда

имеет меру

.
По запросу я могу его доказать. В книгах не нашёл, хотя где-то должно быть.