Откладываем значения некоторого доверительного интервала.
У Вас неверные представления, что такое доверительный интервал.
Для простоты предположим, что есть случайная величина

, которая с вероятностью

(то есть такая честная монетка, где орел - нОль, а рЕшка - единица).
Тогда можем
точно посчитать математическое ожидание

А теперь представим, что мы
не знаем, что монетка честная. Тогда стоИт вопрос - как оценить матожидание?
Всё, что нам известно, это некоторая выборка
конечного размера.
Хорошая оценка матожидания - среднее по выборке.
Кинули пять раз, получили

, среднее

Можем ли мы считать, что
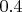
- это и есть матожидание? Нет, не можем. Так как матожидание равно

, а такую выборку получить вполне вероятно.
Или даже так, получили выборку

, среднее

. И что нам думать, про "честность" монетки? Получить такую выборку при честной монетке

. Не так уж мало.
Так вот
а) когда мы делаем
оценку матожидания случайной величины в виде среднего по выборке (или какого-то другого статистического параметра) - это называется точечная оценка.
б) но мы можем более сложными методами посчитать
интервальную оценку: указать интервал, в который попадает оцениваемая величина с заданной надежностью.
Почитайте книгу Владимир Савельев. "Статистика и котики". А там уже можно будет переходить и к учебникам по теорверу и матстатистике
