вот мы облучаем молекулу электромагнитными волнами, она переходит с нулевого колебательного уровня на n-й, поглощается квант строго определённой энергии, почему молекула никогда не переходит в суперпозицию?
Как раз переходит:
Написанные выше формулы - для ситуации без облучения. Осциллятор там предоставлен сам себе, не возмущён никаким внешним воздействием. Если же на осциллятор начинает действовать переменное (во времени) внешнее поле, то в гамильтониан осциллятора прибавляется "возмущение" - оператор энергии взаимодействия (interaction)

с этим полем.
Тогда решения нестационарного у.Ш. можно искать по-прежнему в виде суперпозиции невозмущённых стационарных состояний, но теперь уже с зависящими от времени коэффициентами

Физический смысл этого вот какой:
Допустим, что до того, как возмущение включилось, осциллятор достоверно (т.е. с вероятностью, равной единице) находился на нулевом уровне,

Значит, в это раннее время

а остальные коэффициенты суперпозиции равны нулю:

с номерами

Затем, когда уже включилось возмущение, в спектре частот которого есть в том числе и частота, равная частоте осциллятора
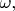
коэффициент

со временем увеличивается (по модулю), а

уменьшается. Физически это означает, что увеличивается вероятность

обнаружить осциллятор на уровне

а вероятность того, что он всё ещё остаётся на уровне

соответственно уменьшается.
Далее может делаться отличным от нуля и

- это будет означать, что появляется ненулевая вероятность

обнаружить осциллятор перешедшим уже с уровня

на

И так далее. Обратные переходы, с высоких уровней на низкие, при учете взаимодействия с переменным полем тоже возможны. В итоге, когда внешний источник возмущения выключится, осциллятор оказывается в состоянии-суперпозиции - с некоторым распределением вероятностей

быть обнаруженным на том или ином уровне.
Вычисляют

методом "теории возмущений": каждая функция

ищется в виде суммы нескольких первых членов ряда по степеням

В задачах со слабым возмущением (такие часто встречаются) достаточно низших приближений теории возмущений: при этом в ответе один из итоговых коэффициентов

оказывается намного больше (по модулю), чем другие. Тогда мы пренебрегаем другими и говорим, что осциллятор переходит за данное время с начального уровня на n-й уровень с вероятностью

В общем же случае переменное поле может с разными вероятностями вызывать разные переходы.
Подобный подход применяют во многих нестационарных задачах (другого-то вроде бы нет); полагаю, что и в фотохимии, в принципе, ситуация аналогичная.
B3LYP, да, коллеги верно пишут - попотеть над учебниками совершенно необходимо, чтобы освоить физику. Если будете лишь гуглить, то в математике и физике в лучшем случае достигнете уровня, как говорится, "инвалида интернетного образования" :) (На этом откланиваюсь из данной темы; пересказывать почти целиком учебники на страницах форума не вижу смысла.)



