Всем привет. Пусть есть последовательность событий

.
Определение верхнего предела этой последовательности
в интерпретации теории множеств:

Соответствующее определение в
интерпретации теории вероятностей: множество исходов

, которые бесконечное число раз (бесконечно часто) встречаются в последовательности

(© Ширяев, Вероятность-I)
Как я понимаю, определение в
интерпретации теории множеств можно переформулировать в

Пусть для большей ясности

для всех
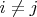
. Тогда

Как должно прозвучать это в интерпретации теории вероятностей?



