Если маршрут зациклился, то на некоторой итерации, неизбежно сокращение "расстояния" (нового кратчайшего пути) между нашими клетками
Да, так работает. Формально, возьмем пару клеток, которые нельзя синхронизировать, и из всех пар выберем с минимальной длиной пути между клетками, а из всех таких - в которых при шахматной лексикографической нумерации бОльшая клетка как можно позже. Заметим, что если мы по кратчайшему пути ведем меньшую клетку в большую, то на каждом шаге расстояние между ними не увеличивается (потому что меньшая клетка на каждом шаге приближается к изначальному положению большей на

, а большая удаляется от него не больше чем на

), причем сохраняется оно только если большая клетка ни разу не упирается в стену. Ну и дальше противоречие: у нас либо большая клетка хоть раз упиралась в стену (и тогда расстояние уменьшилось), либо ни разу не упиралась (и тогда она сдвинулась на тот же вектор, что и меньшая, и стала лексикографически больше).
Итого на текущий момент решены вроде бы 1,2,3,4, 6а и 9.
-- 17.10.2023, 16:47 --8. Левша и невидимая блоха на плоскости играют, ходя по очереди. Очередным ходом Левша проводит прямую, а блоха совершает прыжок длины 1, не пересекающий ни одной прямой. Если таких прыжков нет, блоха проигрывает. Может ли Левша выиграть, как бы не играла блоха?
Вроде то же самое. Предполагаем, что она в квадрате
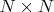
, очерчиваем его с отступами, заполняем сеткой с шагом

, дальше предполагаем, что была в квадрате

, очерчиваем квадрат, куда могла упрыгать, и т.д.
Еще пропустил решение 10 от
TOTAL. Остались 5, 6б, 7.



