Подскажите пожалуйста, можно ли представить цепное правило следующим образом.
Есть функция

, есть

, есть их композиция

. Производная композиции есть

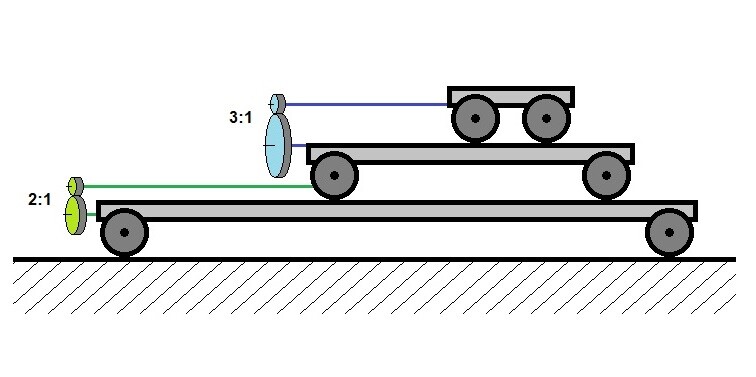
Есть три тележки, которые катятся одна по другой. Ведущие колеса соединены гибкими валами с редукторами

и

. Толкая нижнюю тележку, мы приводим в движение верхние. Тележки могут свободно перемещаться друг относительно друга, но скорость вращения колес задается редукторами.
Нижнюю тележку толкаем со скоростью

, средняя толкается в два раза быстрее.
Верхняя толкается в три раза быстрее относительно средней. Нижнюю тележку мы при этом как бы отрезаем, верхняя катится по средней "независимо" от нижней.