Мне все же кажется, что вы доказываете что-то другое, либо я фундаментально вас не понимаю.
Давайте для удобства будет считать
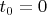
. Соответственно, нам нужно доказать, что для заданого

найдется такое

, что, какая бы у меня ни была
![$x(t)\in C[0,1]$ $x(t)\in C[0,1]$](https://dxdy-04.korotkov.co.uk/f/b/7/8/b78f20b7d270a0cdd622ce8fe8b0291b82.png)
(равная, впрочем, нулю вне отрезка
![$[0,h]$ $[0,h]$](https://dxdy-01.korotkov.co.uk/f/c/a/e/caef84774dafacc0ebd4d820b6d8147c82.png)
), все равно

.
(Оффтоп)
То есть, по сути, мы хотим доказать, что даже если

, но вне небольшого отрезка функция равна нулю, то она будет "недалека" от тождественного нуля. Это, конечно, будет противоречить нашему предположению о том, что поточечную сходимость можно рассматривать как сходимость по метрике, т.к. можно будет придумать такую последовательность, что в точке

она будет далека от нуля, а в то же время по метрике сходиться к тождественному нулю.
И вы доказываете это, предъявляя некую последовательность, которая поточечно сходится к нулю и равна нулю вне сжимающихся отрезков... я не понимаю, как это доказывает наше утверждение



