Градиент от интеграла по поверхности

[intex2dx]

Решаю такую задачу:
Пусть $\Omega$ - телесный угол, под которым виден контур $L$, то есть:

$$\Omega = \int\limits_{S} \frac{\cos(\widehat{\vec{r}, \vec{n}})}{r^2}dS$$

Здесь поверхность $S$ натянута на $L$. Нужно доказать, что:

$$\oint\limits_{L} \frac{[\vec{dl}, \vec{r}]}{r^3} = \operatorname{grad}{\Omega}$$

Я решил применить к интегралу по контуру формулу Стокса:

$$\oint\limits_{L} \frac{[\vec{dl}, \vec{r}]}{r^3} = \int\limits_{S} \left[[\vec{n}, \vec{\nabla}], \frac{\vec{r}}{r^3} \right] dS = \int\limits_{S} \vec{\nabla} \left(\vec{n}, \frac{\stackrel{\downarrow}{\vec{r}}}{r^3} \right)dS - \int\limits_{S}\vec{n} \left(\vec{\nabla}, \frac{\vec{r}}{r^3} \right)dS = \int\limits_{S} \vec{\nabla} \left(\vec{n}, \frac{\stackrel{\downarrow}{\vec{r}}}{r^3} \right)dS $$

С другой стороны, если взять градиент телесного угла, получим:

$$\operatorname{grad}{\Omega} = \operatorname{grad}\left(\int\limits_{S} \frac{(\vec{r}, \vec{n})}{r^3} dS \right) = \int\limits_{S} \vec{\nabla} \left(\vec{n}, \frac{\vec{r}}{r^3} \right) dS$$

То есть отличие обеих частей в том, что в первом случае набла применяется к скалярному произведению в предположении, что $\vec{n} =\operatorname{const}$ (это обозначено стрелочкой $\downarrow$), а во втором случае набла применяется "честно", с учётом того, что $\vec{n} = \vec{n}(\vec{r})$.
Возможно причина в том, что я неправильно взял градиент от интеграла по поверхности. Прошу подсказать, в чём моя ошибка.

[svv]

Давайте сначала исправим ошибку в формуле, которую надо доказать. Для этого рассмотрим простой случай. Наблюдатель находится в начале координат $O$. Контур описывается системой
$z=\operatorname{const}>0$
$x^2+y^2=\operatorname{const}>0$
Для наглядности, ось $Oz$ направлена вертикально вверх; контур — это окружность в горизонтальной плоскости над головой наблюдателя; центр окружности лежит на $Oz$; считаем, что натянутая на контур поверхность лежит в той же горизонтальной плоскости, т.е. это круг.

Будем говорить, что произвольный вектор $\mathbf a$ направлен "вверх" (в кавычках), если $a_z>0$, и "вниз", если $a_z<0$.

Нам нужно решить:
1) направлен ли вектор $\mathbf r$ от наблюдателя к точке поверхности $S$ ("вверх"), или от этой точки к наблюдателю ("вниз");
2) направлен ли вектор нормали $\mathbf n$ к поверхности $S$ от наблюдателя ("вверх"), или к наблюдателю ("вниз").
Естественно потребовать, чтобы $\Omega>0$, тогда $\mathbf r\cdot\mathbf n>0$, и либо оба вектора направлены "вверх", либо оба "вниз". Вы можете выбрать любой вариант (сообщите, какой).

Чтобы применить теорему Стокса, надо согласовать направление обхода контура с выбором $\mathbf n$ по правилу правого винта. Скажем, если $\mathbf n=\mathbf e_z$, то $d\mathbf l$ сонаправлен (а не просто параллелен) $\mathbf e_\varphi$.

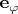
Если сам наблюдатель будет перемещаться вверх, он будет приближаться к контуру и видеть его под всё большим телесным углом, следовательно, $\operatorname{grad}\Omega$ в начале координат направлен "вверх".

Задание. Убедитесь, что при любом выборе 1,2 формула, которую надо доказать, даёт неправильный знак, поскольку $d\mathbf l\times\mathbf r$ направлен "вниз".

[intex2dx]

Да, тут мне стоит немного скорректировать формулировку задачи, ибо я допустил в ней некоторые ошибки. Возможно, будет немного понятнее, если описать физическую суть доказываемого соотношения. Есть контур, на нём изначально задано направление обхода (направление текущего тока). С этим направлением связана правовинтовая нормаль. Всё, направления $\vec{dl}$ и $\vec{n}$ больше не трогаем.

Телесный угол определяется в соответствии с этой нормалью, при этом $\vec{r}$ всегда направлен от наблюдателя к поверхности/к контуру. То есть телесный угол может быть и отрицательным. В частности, в Вашем примере, если ток течёт по окружности так, что $\vec{n} = \vec{e}_z$, то если смотреть снизу, то телесный угол положительный, а сверху он будет отрицательный. Зато $\operatorname{grad}{\Omega}$ будет всегда смотреть вверх (туда же, куда смотрит магнитное поле на оси витка с током).
В этих терминах соотношение, которое мы должны доказать, выглядит так:

$$\oint\limits_{L} \frac{[\vec{dl}, -\vec{r}]}{r^3} = \operatorname{grad}{\Omega}$$

[svv]

Прекрасно. Теперь опишу обозначения (или даже "технику"), которые мне кажутся проясняющими.

Пусть $\mathbf x$ — радиус-вектор точки, где находится наблюдатель, $\mathbf y$ — радиус-вектор точки на поверхности/контуре.

intex2dx в сообщении #1603983 писал(а):

$\vec{r}$ всегда направлен от наблюдателя к поверхности/к контуру

Хорошо. Этому выбору соответствует $\mathbf r=\mathbf y-\mathbf x$.

Некоторые величины зависят от $\mathbf x$ (например, $\Omega$), некоторые от $\mathbf y$ (например, $\mathbf n$), а вектор $\mathbf r=\mathbf y-\mathbf x$ зависит и от $\mathbf x$, и от $\mathbf y$. А потому надо различать два дифференциальных оператора, две наблы (записаны в декартовых координатах):
$\begin{array}{l}\nabla_{\mathbf x}=\mathbf e_1\frac{\partial}{\partial x_1}+\mathbf e_2\frac{\partial}{\partial x_2}+\mathbf e_3\frac{\partial}{\partial x_3}\\[1ex]\nabla_{\mathbf y}=\mathbf e_1\frac{\partial}{\partial y_1}+\mathbf e_2\frac{\partial}{\partial y_2}+\mathbf e_3\frac{\partial}{\partial y_3}\end{array}$

Ясно, что $\operatorname{grad}\Omega$ — это $\operatorname{grad}_{\mathbf x}\Omega$, а вот в формуле Стокса фигурирует $\nabla_{\mathbf y}$:
$\oint\limits_{L} d\mathbf l(\mathbf y)\times\mathbf a(\mathbf x, \mathbf y)= \int\limits_{S} (\mathbf n(\mathbf y)\times\nabla_{\mathbf y})\times \mathbf a(\mathbf x, \mathbf y)\;dS(\mathbf y)$
Поскольку формула справедлива при любом фиксированном $\mathbf x$, который здесь является параметром.

Задание. Покажите, что
$\operatorname{grad}_{\mathbf x}\frac 1 r =\frac{\mathbf r}{r^3}$,
но
$\operatorname{grad}_{\mathbf y}\frac 1 r =-\frac{\mathbf r}{r^3}$.
Здесь вычисления приводить не нужно, просто подтвердите, что получилось. И продолжим.

P. S. Вы можете обозначать векторы, а также скалярное и векторное произведение, как Вы привыкли, но я буду по-своему.

[intex2dx]

Теперь я понял свою ошибку - я не разобрался, от какого вектора зависит интеграл, когда мы берём от него градиент (и вообще не ввёл в рассмотрение радиус-вектор $\vec{x}$ наблюдателя). С техническими моментами дальше помощь не требуется, они достаточно просты и понятны для меня. Спасибо за помощь

[svv]

Хорошо.