Добрый день. Мне необходимо доказать следующее утверждение:
Пусть

- гармоническая функция двух переменных (

). Тогда, если точка

лежит внутри контура

, то значение

в точке

равно:

Здесь производная берётся по направлению внутренней нормали к контуру

. (всё дело происходит на плоскости). Вектор

проводится из точки

.
Я пробовал доказать следующим образом. Рассмотрим контур

, представляющий собой контур

вместе с контуром

, где контур

- круговой контур радиуса

, охватывающий точку

.
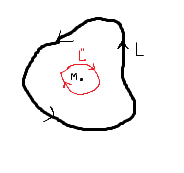
Преобразуем интеграл и применим вторую формулу Грина к области

между контурами

и

:

С другой стороны:

Тогда из формулы:

Получим:

Соответственно, вопрос: почему появляется дополнительный интеграл по

, которого не должно быть в доказываемой формуле?



