Совершенный кубоид

[mathematician123]

Вот параметризация героновых треугольников, использованная в доказательстве:

$$a = mn(p^2 + q^2)$$

$$b = pq(m^2 + n^2)$$

$$c = (mq + np)(mp - nq)$$

Утверждается, что она описывает все героновы треугольники, но это не так. Например, треугольник $(13, 14, 15)$ этими формулами получить нельзя. Зато, если взять $(m, n, p, q) = (2, 1, 3, 2)$, то получим треугольник $(26, 28, 30)$. Значит, в доказательстве Захара в системе (V) для полноты параметризации нужно вводить дополнительную переменную $z$:

$$zd^2 = mn(p^2 + q^2)$$

$$ze^2 = pq(m^2 + n^2)$$

$$zf^2 = (mq + np)(mp - nq)$$

[Andrey A]

mathematician123 в сообщении #1599264 писал(а):

Зато, если взять $(m, n, p, q) = (2, 1, 3, 2)$, то получим треугольник $(26, 28, 30)$. Значит...

Значит соответствующий ему кубоид несовершенен (если верить доказательству). А что, пропорциональный кубоид может оказаться совершенным? Я не понимаю, к чему тут требование полноты. Все те же манипуляции можно провести с Героновой параметризацией (и проводили наверняка), но вывод оттуда сделать трудно. А тут оказалось легче. Впрочем, моё заключение автору известно, беру паузу.

[mathematician123]

Andrey A в сообщении #1599270 писал(а):

Я не понимаю, к чему тут требование полноты.

В доказательстве показано, что треугольник $(d^2, e^2, f^2)$ является героновым. Затем из этого делается вывод о разрешимости системы (V), что в последствии приводится к противоречию. Но вывод о разрешимости системы (V) справедлив только в случае полноты параметризации. А она неполная. Для полноты приходится вводить ещё одну переменную $z$.

Кстати, если проделать с полной параметризацией рассуждения как у Захара, то получим довольно занятную систему: четыре числа $zmn$, $zpq$, $p^2 + q^2$, $m^2 + n^2$ являются точными квадратами и $\gcd(p, q) = \gcd(m, n) = 1$ (это условие на НОД у Захара не используется, но в статье в википедии оно упомянуто).

[Andrey A]

mathematician123 в сообщении #1599274 писал(а):

... вывод о разрешимости системы (V) справедлив только в случае полноты параметризации. А она неполная.

Верно. Но как это может быть, что для треугольника $(26, 28, 30)$ неразрешимость в рациональных числах доказана, а для $(13, 14, 15)$ не доказана? На этот вопрос отвечать неинтересно, понимаю. Хотелось возразить или что-нибудь опровергнуть (выплескивая заодно с водой и младенца). Вообще, я ожидал более оживленного обсуждения.
Ладно. Займемся параметризацией Эйлера, и что значит "она неполная". Пусть дан треугольник с длинами сторон $A,B,C$ и требуется выразить его формулами Эйлера: $A=pq(m^2+n^2),B=mn(p^2+q^2),C=(pn+qm)(pm-qn).$ Положим $\dfrac{m}{n}=x,\dfrac{p}{q}=y.$ Разделив все стороны на $(qn)^2,$ получаем подобный треугольник с рациональными сторонами $a=y(x^2+1),b=x(y^2+1),c=(x+y)(xy-1).$
Заметим, что $\dfrac{a+b}{c}=\dfrac{xy+1}{xy-1},\dfrac{c}{a-b}=\dfrac{x+y}{x-y}.$ Тогда

$$x=\sqrt{\dfrac{(a+b+c)(c+a-b)}{(a+b-c)(b+c-a)}}=\dfrac{m}{n}$$

$$y=\sqrt{\dfrac{(a+b+c)(b+c-a)}{(a+b-c)(c+a-b)}}=\dfrac{p}{q}$$

Параметры под радикалом по понятным причинам можно заменить на целые $(A,B,C),$ пары $(m;n),(p;q)$ считать взаимно простыми. По свойству треугольника Герона радикалы рациональны, и значения параметров $m,n,p,q$ однозначно следуют из несократимых дробей. В чем здесь неполнота, в том что искомый треугольник получаем в некотором масштабе? Ну это старая терка. Если повезет получить $1:1$, взятые в другом порядке $B,C,A$ нарушат идиллию. А пытливый школьник спросит — это метров или сантиметров? И будет прав. Величина кубоида заинтересует ребенка (с человека он или со слона?) или гробовщика (сосна или дуб?), ну и т.д. Нас же интересуют свойства фигур никак не зависящие от масштаба или единиц измерения. Если существует хотя бы один кубоид с рациональными ребрами и диагоналями, то существует бесконечно много подобных ему, обладающих теми же свойствами, в том числе целочисленные. В противном случае не существует ни одного. Параметризации Эйлера и Герона полные, иначе бы гроша ломаного не стоили. А единственное упущение Захара в том, что, допустив существование идеального кубоида, надо было добавить: следовательно существует подобный ему, который описывается параметрами $m,n,p,q,$ а это ведет к противоречию. Так что доказано.

[ozheredov]

(Захар)

Andrey A в сообщении #1599360 писал(а):

единственное упущение Захара

Захар - это с Math Help Planet который? (У него, помнится, терминатор на аватаре.) Он что, реально шарит в математике?

[Andrey A]

(ozheredov)

Да, он самый. Перед этой задачей мы все как дети. А вот поди ж ты...

[Andrey A]

P.S.
Интересно, что сам по себе вопрос существования Геронова треугольника со сторонами-квадратами сложен, но разрешим.

Восемь лет назад scwec нашел тройку $\dfrac{1853^2+4380^2+4427^2}{2} \cdot$ $\dfrac{1853^2+4380^2-4427^2}{2} \cdot$ $\dfrac{1853^2-4380^2+4427^2}{2} \cdot$ $\dfrac{-1853^2+4380^2+4427^2}{2} =32918611718880^2.

Не хватает чуть-чуть: чтобы каждый множитель оказался квадратом.

[Rak so dna]

mathematician123 в сообщении #1599274 писал(а):

Кстати, если проделать с полной параметризацией рассуждения как у Захара, то получим довольно занятную систему: четыре числа $zmn$, $zpq$, $p^2 + q^2$, $m^2 + n^2$ являются точными квадратами и $\gcd(p, q) = \gcd(m, n) = 1$ (это условие на НОД у Захара не используется, но в статье в википедии оно упомянуто).

$z=3,m=3,n=4,p=3,q=4$

Напомнило типичный сюжет ферматиков. Почему люди верят, что старую нерешённую проблему можно пробить страничкой тривиальных школьных рассуждений?

[Andrey A]

Rak so dna
Бог с ними с ферматиками. Доказательство есть, или его нет? На Ваш взгляд, можно даже без аргументации.

[Rak so dna]

Andrey A на мой взгляд нет. mathematician123 провёл рассуждения для полной параметризации и получил разрешимую в натуральных числах систему. Так что противоречий нет.

[mathematician123]

Andrey A в сообщении #1599270 писал(а):

Значит соответствующий ему кубоид несовершенен (если верить доказательству). А что, пропорциональный кубоид может оказаться совершенным?

Andrey A в сообщении #1599360 писал(а):

Верно. Но как это может быть, что для треугольника $(26, 28, 30)$ неразрешимость в рациональных числах доказана, а для $(13, 14, 15)$ не доказана?

Попробую объяснить подробнее

1) В доказательстве Захара и в параметризации Эйлера из статьи в Википедии используются целые числа. Я, когда говорил о неразрешимости, тоже имел ввиду целые числа. Что произойдёт, если перейти к рациональным числам, нужно изучать отдельно.

2) Хорошо, чтобы не возникало путаницы, параметризацию Эйлера будем называть полной. Но она полная не в буквальном смысле, а с точностью до подобия. То есть, если $(a, b, c)$ - треугольник Герона, то существует натуральное $k$, такое что треугольник $(ka, kb, kc)$ описывается параметризацией.

3) Треугольник $(13, 14, 15)$ никакого отношения к вопросу о совершенном кубойде не имеет, так как его стороны не являются квадратами. Я его привёл для примера, что параметризация Эйлера описывает героновы треугольники лишь с точностью до подобия. Полнота параметризации говорит, что существует натуральное $k$, такое что треугольник $(13k, 14k, 15k)$ описывается параметризацией. 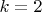Конкретно, можно взять $k = 2$ или $k = 10$. Может быть, есть и другие подходящие $k$. 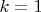Но при $k = 1$ решений нет. Появятся ли они, если разрешить $m, n, p, q$ быть рациональными? Этот вопрос требует отдельного рассмотрения. Зависит от того, разрешима ли в натуральных числах система

$$ \begin{cases} 13K^4 = m_1n_1(p_1^2 + q_1^2) \\ 14K^4 = p_1q_1(m_1^2 + n_1^2) \\ 15K^4 = (m_1q_1 + n_1p_1)(m_1p_1 - n_1q_1) \end{cases} $$

или одна из систем, получаемая перестановкой чисел $(13K^4, 14K^4, 15K^4)$ (системы получены с помощью замен вида $m = \frac{m_1}{K}$).

Andrey A в сообщении #1599360 писал(а):

А единственное упущение Захара в том, что, допустив существование идеального кубоида, надо было добавить: следовательно существует подобный ему, который описывается параметрами $m,n,p,q,$ а это ведет к противоречию.

Описываться должен не кубоид, а треугольник $(d^2, e^2, f^2)$, составленный из квадратов диагоналей. проблема здесь в том, что при масштабировании кубоида в $k$ раз этот треугольник отмасштабируется в $k^2$ раз и получится треугольник $(k^2d^2, k^2e^2, k^2f^2)$. То есть, коэффициент подобия не произволен, а является точным квадратом. Полнота параметризации Эйлера говорит о том, что параметризация описывает треугольник $(zd^2, ze^2, zf^2)$ при некотором натуральном $z$. Если мы хотим спасти доказательство Захара, то необходимо доказать, что число $z$ можно взять равным точному квадрату.

-- 30.06.2023, 10:55 --

Rak so dna в сообщении #1599372 писал(а):

$z=3,m=3,n=4,p=3,q=4$

Я уже потом заметил, что в случае $\{m, n\} = \{p, q\}$ решений много. Но кубоид при таком условии не получится. По идее, если $\{m, n\} \ne \{p, q\}$, решений должно быть гораздо мешьше.

Rak so dna в сообщении #1599379 писал(а):

mathematician123 провёл рассуждения для полной параметризации и получил разрешимую в натуральных числах систему. Так что противоречий нет.

Эта система является следствием и не учитывает все условия. Так что да - даже если попытаться применить рассуждения Захара в исправленном виде, то противоречия не получается.

[Andrey A]

Я прошу учесть только одно. Из существования совершенного кубоида со сторонами $a,b,c,$ следует существование подобного с.к. со сторонами $3a,3b,3c.$ Число $3$ не является квадратом. Если это ведет к противоречию, то либо тут уже доказательство невозможности с.к., либо противоречия у нас в голове. И то и другое не в его пользу. Впрочем, сам он тоже у нас в голове, даже если существует )

[Руст]

Если (a,b,c) совершенный кубоид, то (da,db,dc) при любом натуральном d так же совершенный кубоид.

[Andrey A]

Руст
Именно так. И выше показано, как найти пропорциональный, который описывается параметрами Эйлера. В дальнейшей схеме никто не сомневается. Но не верят.

[Booker48]

Rak so dna в сообщении #1599372 писал(а):

Почему люди верят, что старую нерешённую проблему можно пробить страничкой тривиальных школьных рассуждений?

Они, конечно, в данном случае тривиальны. Только на то обстоятельство, что квадраты лицевых диагоналей СК образуют геронов треугольник, обратили внимание совсем недавно, а вот Эйлер, который занимался и СК и ГТ, судя по всему, этого просто не заметил.
Да и невозможность равенства суммы двух четвёртых степеней точному квадрату - не совсем школьное знание, хотя олимпиадники, конечно, в курсе.
И соединить эти два факта Захару как-то в голову пришло, пусть, возможно и не до конца у него получилось, хотя мне очень хочется верить, что недостатки устранимы.
Чем-то напоминает историю с ВТФ, когда Фрай и Рибет устанавливали параллели между модулярными формами и эллиптическими уравнениями. )))