В разбираемой
статье Geoffrey Exoo читаем:
Цитата:
С помощью компьютера легко убедиться, что нет монохроматических (полных) подграфов

в этой раскраске.
А зачем привлекать компьютер? Я распечатал две копии рис. 2,
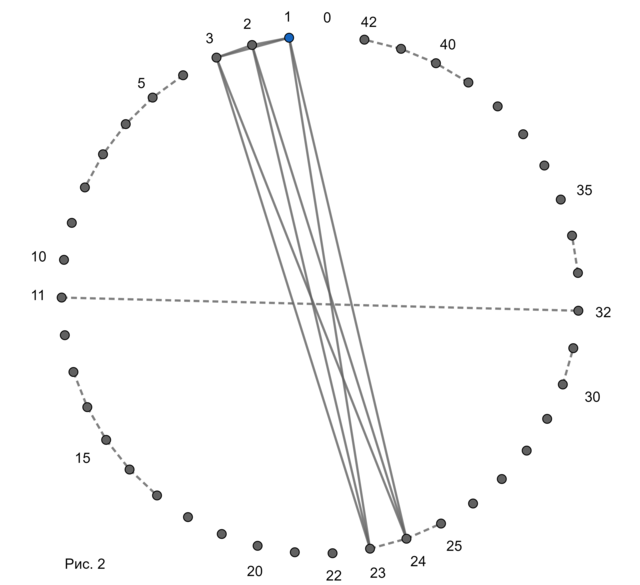
из одной вырезал фигуру, ограниченную вершинами

(что-то вроде стрелки компаса), чуть-чуть укоротил ее на концах (чтобы они не закрывали окружность), совместил ее на фанерке с ней же самой на целой копии рисунка, нашел центр окружности (он находится на прямой, проходящей через вершину

и между вершинами

), вбил в него иголку (можно гвоздик), стал вращать "стрелку" и убедился, что везде либо с одного, либо с другого конца "стрелки" находится по крайней мере одна пунктирная дуга длиной

, либо длинные ребра совмещаются с пунктирным ребром

.
Исключение составляет зона с убранной нулевой вершиной (deleted vertex zero), но в ней нет полных пятерок (правда, тут надо понимать, что все те ребра, не инцидентные нулевой вершине, которые уже были до ее удаления, остаются, то есть соединяют те же вершины, что и соединяли).
Разве этого не достаточно?