Не знаю, писать сюда или сразу в дискуссионный раздел

Но если серьезно, вроде бы мой вопрос вполне математический.
Мне нужна общая теория о том, как создавать математические нотации. Я давно заметил, и с каждым днем все сильнее и сильнее убеждаюсь, что многие вещи в математике сложны не потому что они сложные, а просто потому что в той или иной области нету хорошей системы обозначений (а часто и понятий). Я могу сказать более резко:
все нотации, во всех знакомых мне разделах математики, которые я когда либо видел, невероятно бедны. Любой, кто изучал топологию, согласится со мной в том, насколько проще становятся там доказательства, если использовать развитую теоретико-множественную нотацию. Любой, кто изучал линейную алгебру, согласится, что огромное количество доказательств можно провести гораздо проще, если владеть более развитой общеалгебраической теорией и соответствующей нотацией. Внутри общей алгебры такое встречается тоже повсеместно. Я как-то пытался доказать невырожденность какой-то матрицы (на начальном этапе построения теории), очень заколебался это делать, но как-то все же доказал. Потом, через какое-то время, я вернулся к той проблеме и понял, что матрицу можно разложить в произведение довольно тривиальных матриц, потом просто взял и посчитал определитель произведения. Он оказался ненулевой, а значит первоначальная матрица невырожденна. Какой смысл был в том сложном первоначальном доказательстве? Да никакого смысла не было. Пустая трата сил и времени. И таких примеров у меня накопилась уйма.
Доказать теорему - это примерно как прыгать с камня на камень в попытке пересечь горную речку. Слаборазвитые теории - это когда камней мало и они находятся далеко друг от друга. Приходится очень сильно напрягаться, чтобы перепрыгнуть с одного камня на другой. Но когда в теории есть развитая система самозамкнутых понятий и развитая система обозначений, то мы имеем вместо редких камней проложенную брусчатку, ходить по которой одно удовольствие.
Как строить математические теории - это отдельная большая тема (которая мне тоже интересна). Но сейчас я готов ограничиться более частной темой, связанной с нотациями. В одной и своих предыдущих тем я уже искал кое-что подобное:
Допусти есть две суммы: одна по множеству

, другая по множеству

. Мы хотим найти сумму по множеству

, как-нибудь образованному от множеств

и

. Ладно, если это просто пересечение там или объединение. А если мы, например, образуем множество

с помощью какой-нибудь сложной формулы с большим числом разных теоретико-множественных операций. Пусть нам повезло и есть какое-нибудь одно объемлющее множество. Мы же знаем, что булеан образует алгебру над

относительно симметрической разности и пересечения (и понятно какого умножения на скаляры). Было бы здорово, если бы были теоремы, связывающие суммирование вот с этой алгеброй. И можно было бы считать какие-нибудь нетривиальные суммы, используя то свойства сумм, то делая вычисления в этой алгебре, переходить из одного "мира" в другой и по итогу приходить к чему надо.
Это просто пример того, какую нотация я счел бы развитой.
Ну или можно общую топологию взять. Всем известны обозначения типа

и

. С их помощью можно составлять разные формулы типа

и прочие. Но можно задать вполне резонный вопрос: как ведет себя замыкание при утончении топологии. И если попробовать ответить на этот вопрос, то придется произносить слова в духе: "замыкание в первой топологии представимо как дополнение к некоторому открытому в первой топологии множеству. раз оно открыто в первой топологии, то открыто и во второй, а значит это замыкание в первой топологии будет замкнуто во второй топологии и будет содержать подлежащее множество; следовательно, замыкание во второй топологии, как минимальное замкнутое множество, содержащее подлежащее множество, будет входить как подмножество в замыкание в первой топологии. таким образом, при утончении топологии замыкание может, разве что, уменьшится." Невероятно душный текст. Основная его проблема в том, что произносится слишком много букв, вместо того, чтобы написать короткую строчку в подходящей нотации (сравните, например, с доказательством того, что для любого множества его граница и граница его дополнения совпадают - оно делается вообще без единого слова - просто небольшая строчка; совсем другой коленкор). Во первых, раз замыкание - это минимальное замкнутое множество, содержащее подлежащее множество, а внутренность - это максимальное открытое подмножество,
где нотация со значками 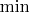
и
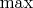
?? Во-вторых, вложенные друг в друга топологии образуют частичный порядок -
где нотация со значками типа 
для топологий?? Таких нотаций нету. А это я просто ткнул пальцем в более менее случайную теорему из простейшей общей топологии.
Таких примеров очень много. Я хочу почитать про подходы о том, как сделать нотацию, если ее нету. Я уверен, что эта область знаний является абсолютно строгой и математичной (я даже примерно представляю, какие методы там могут использоваться). В общем, надеюсь, что более-менее описал проблему.