Но пополнение

, я так понимаю, совпадает с

.
но

Я так понимаю, мы оба описались и подразумевается в этих случаях без

.
Что у них совпадают сопряженные, доказать легко, что

чуть сложнее
Навело ваше сообщение меня на некоторые мысли... Во-первых, я осознал, что

- сепарабельно. Ну то есть если бы оно было несепарабельно, наверное, у вас бы не возникало вопросов о его изоморфизме с

. В том плане, что до сегодняшнего дня я как-то assumed, что оно несепарабельно (как

). Но на самом деле сейчас я даже понимаю, как доказать сепарабельность: возьмем всюду плотное счетное множество в

и прибавим к каждой последовательности заданное рациональное число. Тогда получим счетное множество последовательностей, сходящихся к этому числу, и сколь угодно близко приближающих любую последовательность, сходящуюся к этому числу. Далее поступим так для всех рациональных чисел, и вуаля, правильно я размышляю?
Во-вторых, опять же, я впервые осознаю, что

(кстати, из этого в свою очередь следует сепарабельность

). Да, на самом деле, тут и доказывать особо нечего, доказывается так же, как и для

(и даже со ссылкой на то доказательство: любой элемент

"является" (в смысле изоморфизма) элементом
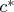
, а другие не могут быть, потому что они не будут работать уже на

, а

).
В-третьих, над ситуацией, что
нужно поразмыслить... как-то сильно они непохоже, мне кажется, должно быть какое-то тривиальное доказательство...
-- 01.04.2023, 14:24 --Кстати, а не следует ли их "не-изоморфизм" из того, что они по-разному вкладываются в

, которое их двойное сопряженное? впрочем, совсем не очевидно, что следует...



