|
i |
Ende
Название темы изменено по просьбе топикстартера. |
АннотацияДоказательство гипотезы Коллатца. Поиск различных зависимостей между натуральными числами. Построение матрицы спуска. Проверка полученных результатов на компьютере. Ключевые слова: гипотеза Коллатца, рекурсия, матрица спуска.
§1. ВведениеГипотеза Коллатца - это одна из нерешенных проблем математики. Получила широкую известность благодаря простоте формулировки:
Берём любое натуральное число

; Если оно чётное, разделим его на 2, а если нечетное, то умножаем на 3 и прибавляем 1 (получаем

); Над полученным числом выполняем те же самые действия, и так далее.
Какое бы начальное число

мы ни взяли, рано или поздно мы получим единицу, - так гласит гипотеза. И надо это доказать.
Давайте посмотрим на последовательности в гипотезе Коллатца (

):
3, 10, 5, 16, 8, 4, 2, 1
5, 16, 8, 4, 2, 1
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
13, 40, 20, 10, 5, 16, 8, 4, 2, 1
15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
21, 64, 32, 16, 8, 4, 2, 1
23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
§2. Таблица нечетных чисел
Вопрос. Можно ли по этой таблице спуститься к 1? Да, можно.
Это не просто таблица, это матрица спуска к единице.
Спуск выглядит следующим образом:

Для спуска к единице требуется всего два правила. Это "шаг назад" и правило
 §3. Шаг назад
§3. Шаг назадШаг назад в гипотезе Коллатца выглядит следующим образом, пусть

- нечетное число, тогда:
- Чтобы получить предыдущее мы должны умножить

*2.
- Предположим, перед

находится нечетное число

. Тогда справедливо равенство:

- Получаем

- Результат

будет целым только в том случае, если

.
Тогда для

удвоим количество четных чисел:
- Умножаем

на 2, и снова на 2.
- Предположим, перед
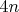
находится нечетное число

. Тогда справедливо равенство:

- Получаем

- Результат

всегда будет целый для

.
Таким образом мы установили зависимость одного нечетного числа от другого.
Эта зависимость не простая. Она рекурсивная. Каждое нечетное число цепляет другое пока выполняется условие (шаг рекурсии):

Итак, в таблице:

- это шаг назад,

- это нечетное число,

- нечетное число для случая


- последовательность чисел, привязанная к

.
§4. Правило 1/3 (одна треть)Рассмотрим полученные формулы с другого ракурса:

Не будем обращать внимание на

, как пренебрежительно малое число, и сосредоточимся только на

и

. Это ни что иное, как уменьшение/увеличение числа n на

. Такое уменьшение/увеличение будем называть "правилом 1/3".
§5. Особая связь ( )
)Давайте посмотрим на последовательности для 7 и 29:

Чтобы подняться из числа 11 на шаг наверх, нам нужно решить равенство

.
А что если мы хотим еще выше? Давайте решим его для

:




Да, всё сходится:

Но давайте возьмем другой пример:

Чтобы подняться из числа 7 на два шага наверх, нам нужно решить равенство

.
А что если мы хотим еще выше? Давайте решим его для

:




Да, всё верно:

Заметьте, мы специально взяли два примера (7 и 11), которые дают нам разный остаток от деления на три, но получили одну и ту же зависимость.
Сформулируем её так: Если число

связано с другим числом

по правилу 1/3, то число

также будет связано с его производным

по правилу

.
Другими словами, нечетные числа

и

спускаются к единице по той же последовательности, что и число

.
Важно понимать, что применяя правило

мы заменяем одно нечетное число на другое, но спуск к единице не меняется.
 §6. Матрица спуска
§6. Матрица спускаМы проверили нашу матрицу спуска для чисел от 1 до 1000000000 на компьютере.
Все числа гарантированно спускаются к единице по заданным в матрице правилам (1/3 и

). Каких-либо других правил, связывающих нечетные числа, мы не обнаружили.
Это означает, что мы можем убрать все чётные числа в последовательностях Коллатца, и оперировать только лишь правилами 1/3 и

.
§7. Лучший пример - число 27Давайте сформируем настоящую (истинную) последовательность для 27, используя только лишь правила 1/3 и

:
27

41

31

47

71

107

161

121

91

137

103

155

233

175

263

395

593

445

111

167

251

377

283

425

319

479

719

1079

1619

2429

607

911

1367

2051

3077

769

577

433

325

81

61

15

23

35

53

13

3

5

1.
Для чисел 3077, 2429, 445, 325, 61, 53, 13, 5 - мы воспользовались правилом

, в остальных случаях 1/3. Мы получили точно такую же последовательность спуска к единице, но все чётные исчезли.
§8. Доказательство гипотезы КоллатцаГипотеза выполняет действия

и

, тогда обратные действия:

и

*2.
Сформулируем это так: Возьмем любое натуральное число

; Отнимем из него единицу

; Если результат деления

будет целый, тогда это будет следующее число; Если нет, то умножаем

на 2; И вообще, всегда умножаем

на 2 для порождения всё новых и новых веток.
Посмотрим на последовательности по данной схеме:
1, 2, 4, 1
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 7, 14, 28, 9
1, 2, 4, 8, 16, 5, 10, 20, 40, 13, 26, 52, 17, 34, 11, 22, 44, 88, 29, 58, 19
Обратим внимание, что это обычная последовательность Коллатца, только она развернута в обратном направлении и учитывает все числа, все ветки и все ответвления. Распишем это более подробно.
Выполним преобразование для 1:
Число 1. Умножаем на 2. Получаем 2.
Выполним преобразование для 2:
Число 2. Умножаем на 2. Получаем 4.
Выполним преобразование для 4:
Число 4.

.
Число 4. Умножаем на 2. Получаем 8.
Выполним преобразование для 8:
Число 8. Умножаем на 2. Получаем 16.
Выполним преобразование для 16:
Число 16.

.
Число 16. Умножаем на 2. Получаем 32.
Итак, мы на пороге первой развилки! 1, 2, 4, 8, 16 - здесь у нас развилка на 5 и 32.
Зайдем на развилку 5:
1, 2, 4, 8, 16, 5, 10 - здесь у нас снова развилка на 3 и 20.
1, 2, 4, 8, 16, 5, 10, 3, ...
1, 2, 4, 8, 16, 5, 10, 20, ...
Вернемся к числу 32:
1, 2, 4, 8, 16, 32, 64 - здесь у нас снова развилка на 21 и 128.
1, 2, 4, 8, 16, 32, 64, 21, ...
1, 2, 4, 8, 16, 32, 64, 128, ...
На этом остановимся.
Далее мы рассмотрим множество следующего вида:
1
1, 2
1, 2, 4
1, 2, 4, 1
1, 2, 4, 8, 16
1, 2, 4, 8, 16, 5
1, 2, 4, 8, 16, 32
1, 2, 4, 8, 16, 5, 10
1, 2, 4, 8, 16, 5, 10, 3
1, 2, 4, 8, 16, 5, 10, 20, 40
1, 2, 4, 8, 16, 5, 10, 20, 40, 13
...
Каждый элемент этого множества - это последовательность, образованная очередным шагом по обратной схеме.
Применим к этому множеству бесконечное умножение на 2, и продолжим каждую последовательность:

Таким образом, мы приходим к выводу, что выбирая любое натуральное число

в гипотезе Коллатца, мы на самом деле выбираем элемент из этого множества. Потому что каждое нечетное число в этом множестве - это шаг рекурсии:

А каждое чётное число образовано от нечетного простым умножением на 2.
Таким образом, гипотеза Коллатца - это развернутая в обратном направлении рекурсия.
Для доказательства гипотезы Коллатца нам потребуется:
- Построить множество всех вариантов последовательностей Коллатца, что мы и сделали.
- Показать, как все последовательности Коллатца начинаются с единицы, что мы и сделали.
- Ответить на вопрос, есть ли числа, которые попадают в

, но не попадают в

?
Таких чисел нет, потому что рекурсивное правило

это зеркальная копия

.

.
Это одна и та же рекурсия, просто развернутая в разные стороны. Выполняя одни и те же действия, нельзя сойти с одного и того же пути. Если рекурсия начинается с единицы, то она всегда в неё возвращается (см. книгу С.Клини, Введение в метаматематику, [гл. IX, §46]).
Все последовательности зеркальны, идентичны и обладают одинаковыми свойствами. И мы можем это легко проверить.
§9. Шаг впередПусть

- нечетное число, тогда чтобы двигаться вперед по правилу

мы должны:
- Отнять от

единицу

и разделить на три. Но если мы отнимем от нечетного числа единицу, то мы получим чётное. Четное не делится на три.
- Тогда у нас остается только один вариант, умножить

*2.
- Предположим, после

находится нечетное число

. Тогда справедливо равенство:

.
- Получаем

- Результат

будет целым только в том случае, если

.
Тогда для

удвоим количество четных чисел:
- Умножаем

на 2, и снова на 2.
- Предположим, после
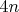
находится нечетное число

. Тогда справедливо равенство:

.
- Получаем

- Результат

всегда будет целый для

.
Тоже самое и с правилом

:

Число 11 порождает две ветки. Зайдем в первую ветку

:

Зайдем во вторую ветку

:



Да, всё верно:

Теперь мы понимаем, почему в гипотезе Коллатца можно заменить нечетное число вида

на его производное и спуск до единицы не изменится. Потому что это раздвоенная ветка одного и того же числа.
Обратим внимание и на цикл «1, 2, 4, 1». Он рождается в обеих схемах, что служит прекрасным доказательством тождественности правил.
Отвечая на вопрос, является ли правило

развернутой в обратном направлении рекурсией

? Мы говорим, однозначно, да.
§10. Последний вопросИ последний вопрос, который мы обязаны задать: Есть ли такое число, которое не входит в рекурсию

?
Предположим, что есть. Но тогда из этого следует, что его нельзя подставить в

. Потому что

- это уже сформированная рекурсия от

.
Таким образом, мы приходим к выводу, что все числа рекурсивно связаны между собой, а правило

перебирает бесконечное количество веток с бесконечным количеством вариантов по mod(3) и умножением на 2. И каждая такая ветка обречена спуститься к единице. Ч.т.д.
---
С уважением,
Автор статьи: Михаил Мартынов, Россия, Оренбург, программист.