Спасибо большое за ответы.
Для попытки обсуждения следующей предполагаемой опечатки в задачнике нам нужно вычислить

и

. Имеем:

,

. А теперь приступаем к обсуждению опечатки. Проверьте, пожалуйста, решение 22.7, о):
Цитата:
Вот ответы из задачников, изданий, как и 2001, так и 2009 годов:
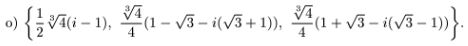
У меня первые 2-то значения сошлись, а для 3-го упорно получается число, сопряженное тому, что приведено в ответе.
(Вот мое решение)
![$\sqrt[3]{1+i}=\sqrt[3]{\sqrt{2}\left(\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}i\right)}=\sqrt[6]{2}\cdot\sqrt[3]{\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}}$ $\sqrt[3]{1+i}=\sqrt[3]{\sqrt{2}\left(\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}i\right)}=\sqrt[6]{2}\cdot\sqrt[3]{\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}}$](https://dxdy-01.korotkov.co.uk/f/4/6/a/46a9224b80b16b29648c57ee55ad115f82.png)
,

,

.
Для

:
![$\sqrt[6]{2}\cdot\left(\cos\dfrac{\pi}{12}+i\sin\dfrac{\pi}{12}\right)=\sqrt[6]{2}\left(\dfrac{\sqrt{2+\sqrt{3}}}{2}+\dfrac{\sqrt{2-\sqrt{3}}}{2}i\right)=2^{\frac{1}{6}}\left(\dfrac{\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}i}{2^{\frac{3}{2}}}\right)=$ $\sqrt[6]{2}\cdot\left(\cos\dfrac{\pi}{12}+i\sin\dfrac{\pi}{12}\right)=\sqrt[6]{2}\left(\dfrac{\sqrt{2+\sqrt{3}}}{2}+\dfrac{\sqrt{2-\sqrt{3}}}{2}i\right)=2^{\frac{1}{6}}\left(\dfrac{\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}i}{2^{\frac{3}{2}}}\right)=$](https://dxdy-01.korotkov.co.uk/f/4/3/8/4384843f26a51431fb840459586a38ee82.png)

![$\dfrac{\sqrt[3]{4}}{4}(\sqrt{3}+1+(\sqrt{3}-1)i)$ $\dfrac{\sqrt[3]{4}}{4}(\sqrt{3}+1+(\sqrt{3}-1)i)$](https://dxdy-01.korotkov.co.uk/f/0/c/3/0c3bacd19c3fce252f125d687ef0559782.png)
как раз и получается упомянутая выше сопряженность с тем, что приведено в ответе. Для двух оставшихся значений

получаем:
для

:
![$\sqrt[6]{2}\cdot\left(\cos\dfrac{3}{4}\pi+i\sin\dfrac{3}{4}\pi\right)=\sqrt[6]{2}\left(-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}i\right)=\dfrac{1}{\sqrt[3]{2}}\left(-1+i\right)=\dfrac{\sqrt[3]{4}}{2}\left(-1+i\right)$ $\sqrt[6]{2}\cdot\left(\cos\dfrac{3}{4}\pi+i\sin\dfrac{3}{4}\pi\right)=\sqrt[6]{2}\left(-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}i\right)=\dfrac{1}{\sqrt[3]{2}}\left(-1+i\right)=\dfrac{\sqrt[3]{4}}{2}\left(-1+i\right)$](https://dxdy-01.korotkov.co.uk/f/c/e/7/ce77d62cb0180a9eee4f5dba44c2c6b082.png)
,
для

:
![$\sqrt[6]{2}\cdot\left(\cos\dfrac{17\pi}{12}+i\sin\dfrac{17\pi}{12}\right)=\sqrt[6]{2}\left(-\cos\dfrac{5\pi}{12}-i\sin\dfrac{5\pi}{12}\right)=\sqrt[6]{2}\left(-\sin\dfrac{\pi}{12}-i\cos\dfrac{\pi}{12}\right)=$ $\sqrt[6]{2}\cdot\left(\cos\dfrac{17\pi}{12}+i\sin\dfrac{17\pi}{12}\right)=\sqrt[6]{2}\left(-\cos\dfrac{5\pi}{12}-i\sin\dfrac{5\pi}{12}\right)=\sqrt[6]{2}\left(-\sin\dfrac{\pi}{12}-i\cos\dfrac{\pi}{12}\right)=$](https://dxdy-02.korotkov.co.uk/f/d/f/f/dff208f7702e635ef537cb93a6a0423582.png)
![$\sqrt[6]{2}\left(-\dfrac{\sqrt{2-\sqrt{3}}}{2}-i\dfrac{\sqrt{2+\sqrt{3}}}{2}\right)=\sqrt[6]{2}\left(-\dfrac{\sqrt{4-2\sqrt{3}}}{2^{\frac{3}{2}}}-\dfrac{\sqrt{4+2\sqrt{3}}}{2^{\frac{3}{2}}}i\right)=$ $\sqrt[6]{2}\left(-\dfrac{\sqrt{2-\sqrt{3}}}{2}-i\dfrac{\sqrt{2+\sqrt{3}}}{2}\right)=\sqrt[6]{2}\left(-\dfrac{\sqrt{4-2\sqrt{3}}}{2^{\frac{3}{2}}}-\dfrac{\sqrt{4+2\sqrt{3}}}{2^{\frac{3}{2}}}i\right)=$](https://dxdy-01.korotkov.co.uk/f/c/6/4/c64cf3d1d3f67cddcd11e9a59a67cd5482.png)
![$\dfrac{\sqrt[3]{4}}{4}(-\sqrt{3-2\sqrt{3}+1}-\sqrt{3+2\sqrt{3}+1}i)=\dfrac{\sqrt[3]{4}}{4}(1-\sqrt{3}-(\sqrt{3}+1)i)$ $\dfrac{\sqrt[3]{4}}{4}(-\sqrt{3-2\sqrt{3}+1}-\sqrt{3+2\sqrt{3}+1}i)=\dfrac{\sqrt[3]{4}}{4}(1-\sqrt{3}-(\sqrt{3}+1)i)$](https://dxdy-01.korotkov.co.uk/f/0/0/7/0071ebe76b57ab727af4bbd93d16fcdc82.png)
, т. е., имеем полное совпадение с тем остальным, что сказано в ответе.
Скажите, пожалуйста, это у меня очередной заскок или это очередная опечатка в задачнике?