Ward, Morgan Euler's three biquadrate problem. Proc. Nat. Acad. Sci. U. S. A. 31, (1945). 125--127.
Ward, Morgan Euler's problem on sums of three fourth powers. Duke Math. J. 15, (1948). 827--837.
The famous problem referred to in the title is that of proving or disproving that a biquadrate is not the sum of three biquadrates. This paper proves that the Diophantine relation
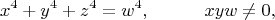
implies (2)
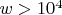
. The basic idea of the proof is set forth in a previous paper [Proc. Nat. Acad. Sci. U. S. A. 31, 125--127 (1945); MR0012104 (6,259e)]. In the present paper a full account of the details is given. The assumption that (1) has a solution leads to the equation
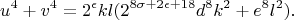
The denial of (2) gives corresponding restrictions on the variables on the right side of (3). All numbers of this form, with these restrictions, are shown not to be the sum of two biquadrates either by using lemmas, small moduli, or in stubborn cases by examining all representations as sums of two sqaures. The extensive calculations involved do not invite further efforts in this direction.



