Начертательная геометрия. Центральная проекция эллипса на плоскость.
Суть задачи в следующем.
Нам известно три точки (A, B, C) и центр эллипса(O). Я проецирую эллипс на плоскость. Нужно найти центр получившегося эллипса.
Я накидал решение:
1) Применяем построение( смотри рисунок) для точек A,B,C,O и находим точку M.
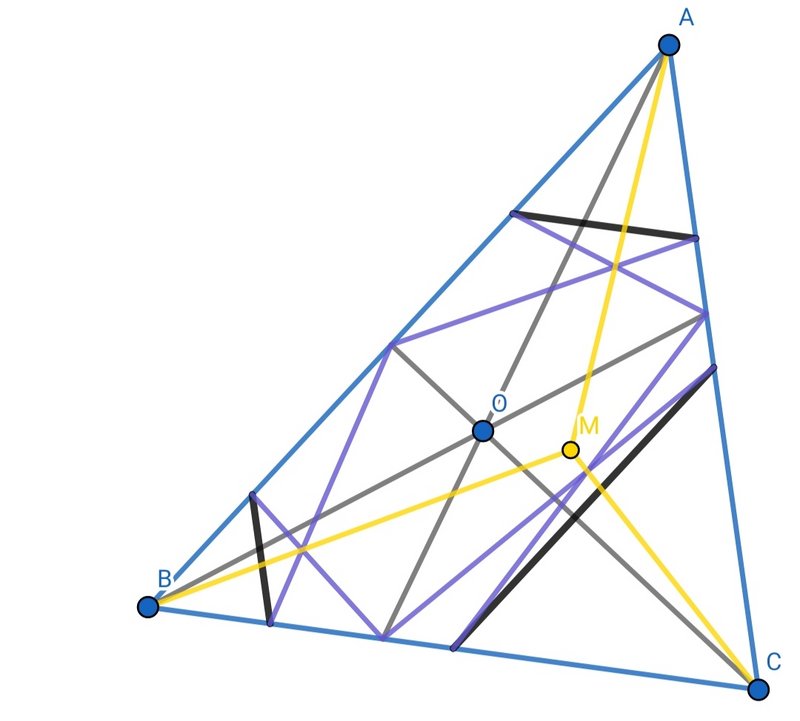
Чёрные прямые симметричны сторонам треугольника относительно точки O.
2) Проецируем точки A,B,C,M на плоскость и получаем новые точки A',B',C',M'.
3) Опять применяем построение для точек A',B',C',M' и находим точку O'. Искомый центр эллипса.
Мне стало интересно есть ли более лёгкий способ решения этой задачи?