Здравствуйте. Я переписал Доказательство более наглядно. Ещё 200 лет назад кто-то совершенно правильно заметил, что надо разделить Доказательство на 2 случая: тройка чисел не делится и делится на показатель степени. Сначала я решил рассмотреть случай, когда одно из чисел тройки делится на показатель степени. Пусть это будет

. Чтобы было легче проверять Доказательство, имеет смысл расписать его для показателя семь. Итак, имеем уравнение
![$x^7+y^7=z^7,z\equiv 0\bmod 7; \eqno [1]$ $x^7+y^7=z^7,z\equiv 0\bmod 7; \eqno [1]$](https://dxdy-02.korotkov.co.uk/f/d/4/a/d4a09c0340b483cd661d7e29e82a141882.png)
. Нужно доказать, что оно не имеет решений в натуральных попарно взаимно простых числах.
Идея в том, чтобы изготовить соотношения для  такие, что при подстановке их в
такие, что при подстановке их в ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) получалось бы ТОЖДЕСТВЕННОЕ РАВЕНСТВО, либо близкое к тождественному!Доказательство Этап 1. С помощью формул Абеля получить соотношения для гипотетических решений уравнения
получалось бы ТОЖДЕСТВЕННОЕ РАВЕНСТВО, либо близкое к тождественному!Доказательство Этап 1. С помощью формул Абеля получить соотношения для гипотетических решений уравнения ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) в натуральных попарно взаимно простых числах!
в натуральных попарно взаимно простых числах!Как и для кубов, доказывается от противного. Пусть существуют такие натуральные попарно взаимно простые числа

, что указанное равенство выполняется. Тогда, как и для кубов, справедлива лемма, правда имеющая некоторые отличия.
Лемма 1.Пусть уравнение

имеет решения в натуральных попарно взаимно простых числах для случая

делится на семь. Тогда верно следующее:
![$$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$ $$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$](https://dxdy-02.korotkov.co.uk/f/9/d/d/9ddcddd02e33953f5df444e9abdbb71882.png)
Доказательство леммы под спойлером
(Оффтоп)
Доказательство леммы.Как в знаменитой телеграмме, переносим

в правую часть, затем по аналогии

. Тогда

 Пусть по определению
Пусть по определению 
, то есть

Так как

Очевидно,

. Получается, что

. Где
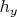
целое число.
Пусть

Так как

. Очевидно,

. Получается, что

. Где

целое число.

. Окончательно получаем

Пусть

делится на

. Тогда


. Поясню последний переход подробнее. Очевидно

Надо ещё выяснить, могут ли

иметь какие-то общие делители. Прежде всего, нужно выяснить, чему вообще равно

. Делается это просто. В силу доказанного выше,


.
Решаем это уравнение относительно

например в wolfram mathematica и получаем, что


.
Отсюда следует, что

нечетно всегда: и когда

четное, и когда

нечетное. При таком раскладе получается, что

не может делиться на

в силу того, что

. Предположим, что

. Тогда

. Но ранее было установлено, что

. Получается, что

. Имеем противоречие, так как

. Имеем, что

.
Аналогично проверяется, что

.

![$\Rightarrow 49\mid z;\eqno[3]$ $\Rightarrow 49\mid z;\eqno[3]$](https://dxdy-02.korotkov.co.uk/f/9/b/c/9bcbfa3ca890e4dd34b5be9ec5a04a0f82.png)
.
Лемма доказана! Этап 2. Вывести такие соотношения для  что при их подстановке в
что при их подстановке в ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) получалось бы тождественное равенство!Лемма 2
получалось бы тождественное равенство!Лемма 2. Существуют такие попарно взаимно простые натуральные числа

, что имеют место следующие соотношения
![$$\left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right.$$](https://dxdy-03.korotkov.co.uk/f/e/4/7/e47a05d7064797f54035f9419db9607a82.png) Доказательство леммы 2
Доказательство леммы 2Вот далее совершенно неочевидный шаг, но такой же, как в доказательстве для кубов. Запишем тождество

.
Конкретно для показателя семь вывод тождества под спойлером.(Оффтоп)
Самое простое - деление уголком по школьному. Как возникла идея записать такое тождество? Из за замены

Итак, как и для кубов, делаем замену

тогда

. В таком случае исходное уравнение принимает вид такой

. Получилось алгебраическое уравнение шестой степени относительно

, свободный член которого имеет должен быть целым. С помощью соотношений из леммы 1, имеем

и тогда свободный член переписывается следующим образом

. Вот и получилось то самое число, из которого тождество взялось. Далее деление уголком хоть по школьному
Умножим обе части тождества на

. Получим

. В силу доказанной леммы, в левой части тождества целое число, значит и последнее слагаемое в тождестве является целым числом. Кто не понял, пояснения под спойлером
(Оффтоп)
А почему в левой части тождества получается целое число? Вот берём соотношения из леммы 1
![$$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$ $$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$](https://dxdy-02.korotkov.co.uk/f/9/d/d/9ddcddd02e33953f5df444e9abdbb71882.png)
Сначала надо обратить внимание, что из первого, второго, третьего и пятого соотношений следует, что

! Затем смотрим на предпоследнее равенство и видим, что оказывается

, стало быть

. Теперь смотрим на пятое и шестое соотношения. Выясняется, что

Поэтому делаем замену переменной

и записываем

Важно понять, какой знак имеет число

. Выразим из последнего равенства

. Получается

. Вернёмся к равенству


Как видите, получилось квадратное уравнение относительно

. Посчитаем его дискриминант.

. Дискриминант представляет из себя в свою очередь квадратное уравнение такое

. Посчитаем его дискриминант.

Теперь решаем каждое квадратное уравнение

Ранее было получено, что

Получается ПТ

.
А дальше рассматриваем 2 случая: 
нечетное и четное. Для начала пусть

четно, а

нечетное. Нужно понять, четное или нечетное число

! Для этого, запишем величину

через

. Получится, что

. Но

нечетное число по лемме 1. Тогда

также нечетные и Пифагорова тройка принимает вид следующий

![$\Rightarrow \left\{
\begin{array}{lcl}
z=\sqrt[6]{7ab}\\
m_0=-(a-b)^2 \\
p=\frac{a(a-b)}{(7(ab))^{5/6}}
\end{array}
\right.$ $\Rightarrow \left\{
\begin{array}{lcl}
z=\sqrt[6]{7ab}\\
m_0=-(a-b)^2 \\
p=\frac{a(a-b)}{(7(ab))^{5/6}}
\end{array}
\right.$](https://dxdy-02.korotkov.co.uk/f/9/b/1/9b161c112f93f6e33fdf3a82ae0d266682.png)
Важно понимать, что

могут не быть натуральными числами, поэтому

Здесь

является возможным общим делителем чисел в ПТ. Сейчас важно узнать, может ли

делиться на

. Для этого распишем

и узнаем, делится ли оно на семь.

.
В силу соотношений
![$\eqno[2]$ $\eqno[2]$](https://dxdy-02.korotkov.co.uk/f/1/3/7/1370d8bfb9aaf2485213813c6e54b0e682.png)
из леммы,

. Раз

не делится на

по лемме 1, то и

не делится и

не делится.
Запишем теперь

в терминах

.

Запишем дробь в терминах соотношений из леммы:

Эта дробь, которая на самом деле является натуральным числом, делится на

, причём не больше и не меньше. Запишем ее же в терминах

. Получим

Раз

делится на

, то

делится на

!
Как найти, чему равно

? Через соотношение для неизвестной

. В терминах

она записывается следующим образом
![$p=\frac{(a-b)\sqrt[6]{7ab}}{7b}=\frac{(a_1-b_1)\sqrt[6]{7a_1b_1\alpha}}{7b_1}; p\in\mathbb{N}\Rightarrow \frac{7a_1\alpha}{b_1^5}\in\mathbb{N}\Rightarrow \alpha=b_1^5 \alpha_2;$ $p=\frac{(a-b)\sqrt[6]{7ab}}{7b}=\frac{(a_1-b_1)\sqrt[6]{7a_1b_1\alpha}}{7b_1}; p\in\mathbb{N}\Rightarrow \frac{7a_1\alpha}{b_1^5}\in\mathbb{N}\Rightarrow \alpha=b_1^5 \alpha_2;$](https://dxdy-01.korotkov.co.uk/f/4/1/3/41325afb08e1688806de263807ae003582.png)
Теперь возникает вопрос, как найти

? Используя факт, что числа

и

являются взаимно простыми в силу леммы 1!

Из леммы 1 следует, что

. Запишем

через

. Получим
![$z+7p=\frac{a_1\sqrt[6]{7a_1b_1^6\alpha_2}}{b_1}=a_1\sqrt[6]{7a_1\alpha_2}$ $z+7p=\frac{a_1\sqrt[6]{7a_1b_1^6\alpha_2}}{b_1}=a_1\sqrt[6]{7a_1\alpha_2}$](https://dxdy-04.korotkov.co.uk/f/3/4/7/347355e20143efc02545f656ce40efb482.png)
. Как уже было показано выше,

, значит

Осталось записать соотношения для

в окончательном виде!
Имеем
![$\left\{
\begin{array}{lcl}
z=\sqrt[6]{7a_1}b_1\\
p=\sqrt[6]{7a_1}\frac{a_1-b_1}{7} \\
(a_1,b_1)=1,a_1,b_1\in \mathbb{N}
\end{array}
\right.$ $\left\{
\begin{array}{lcl}
z=\sqrt[6]{7a_1}b_1\\
p=\sqrt[6]{7a_1}\frac{a_1-b_1}{7} \\
(a_1,b_1)=1,a_1,b_1\in \mathbb{N}
\end{array}
\right.$](https://dxdy-03.korotkov.co.uk/f/e/8/7/e8723a80aac2427f370ac605aacb7a2f82.png) Далее индексы у
Далее индексы у  можно опустить и писать просто
можно опустить и писать просто 
Зная

и

можно найти

. Надо просто записать сумму и произведение

через

и найти

как корни квадратного уравнения. Произведение записывается через соотношение для

,а сумма - через соотношение для

. Я напомню, что в лемме 1 было доказано, что

. Ну и произведение

Осталось выразить

через

и можно решать квадратное уравнение. Из леммы следует, что
![$x+y=7^6C^7\Rightarrow z+7p=7^6C^7\Rightarrow 7C=\sqrt[6]{7a}\Rightarrow C=\frac{\sqrt[6]{7a}}{7};\eqno[2.1]$ $x+y=7^6C^7\Rightarrow z+7p=7^6C^7\Rightarrow 7C=\sqrt[6]{7a}\Rightarrow C=\frac{\sqrt[6]{7a}}{7};\eqno[2.1]$](https://dxdy-04.korotkov.co.uk/f/b/5/a/b5a389c4f66c9d1bdfd65312f3f4da5982.png)
Получаем систему уравнений
![$$\left\{
\begin{array}{lcl}
m^7w^7=(a-b)^7D^{-7} \\
m^7+w^7=(2b-a)\sqrt[6]{7a}\ \eqno[2.2]\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
m^7w^7=(a-b)^7D^{-7} \\
m^7+w^7=(2b-a)\sqrt[6]{7a}\ \eqno[2.2]\\
\end{array}
\right.$$](https://dxdy-02.korotkov.co.uk/f/9/1/7/9175008b409f663845d7754f0ab1e9d682.png)
Находим

как корни квадратного уравнения с помощью теоремы Виета. Результат такой (знаки согласованы, это важно!!!)
![$$\left\{
\begin{array}{rcl}
m^7=\frac{(2b-a)\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
w^7=\frac{(2b-a)\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
\end{array}
\right.$$ $$\left\{
\begin{array}{rcl}
m^7=\frac{(2b-a)\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
w^7=\frac{(2b-a)\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
\end{array}
\right.$$](https://dxdy-04.korotkov.co.uk/f/b/3/f/b3f58ac0b14aadffaa6038d2be1eba5b82.png)
Раз теперь

известны, можно найти

с помощью соотношений из леммы, которые имеют вид
![$\left\{
\begin{array}{lcl}
x=w^7+7p \\
y=m^7+7p\\
p=mwA
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
x=\frac{(a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right. $ $\left\{
\begin{array}{lcl}
x=w^7+7p \\
y=m^7+7p\\
p=mwA
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
x=\frac{(a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right. $](https://dxdy-03.korotkov.co.uk/f/a/c/a/acaa64f90634f36b29ae2d219d33212c82.png)
Знаки опять же согласованы! Осталось записать

через

,
где по определению 
Получится, что

, что следует из двух способов представления числа

через

и

и соотношения
![$\eqno[2.1]$ $\eqno[2.1]$](https://dxdy-03.korotkov.co.uk/f/e/3/1/e317be0f5699d3fb5e460ae55e14507282.png)
, то есть нужны соотношения
![$\eqno[3],[2],[2.1]$ $\eqno[3],[2],[2.1]$](https://dxdy-01.korotkov.co.uk/f/8/3/3/833585a23695b7ac50bf3451085f3c9582.png)
из которых следует, что
![$z=\sqrt[6]{7a}b=7C(7^5C^6-mwD)\Rightarrow b=a-FD$ $z=\sqrt[6]{7a}b=7C(7^5C^6-mwD)\Rightarrow b=a-FD$](https://dxdy-02.korotkov.co.uk/f/9/3/e/93e92692bd18e9382024ba90a16abb9482.png)
и что числа

попарно взаимно простые
Лемма 2 доказана Этап 3. С помощью теоремы косинусов записать Пифагорову тройку, затем составить из неё кубическое уравнение относительно косинуса. Думаю, ясно, что должны выполняться условия

существует треугольник со сторонами

для которого справедлива теорема косинусов

Здесь

это угол между

! Я сразу запишу косинус через

в упрощённом виде, используя
![$\eqno[3]$ $\eqno[3]$](https://dxdy-02.korotkov.co.uk/f/d/0/f/d0fdfb9db4e8f0a96b1632982c3236d582.png)
![$\cos\gamma=\frac{x^2+y^2-z^2}{2xy}=\frac{(a-b)^2\sqrt[3]{7a}-2(a-b)^7D^{-7}}{2((a-b)b\sqrt[3]{7a}+(a-b)^7D^{-7})};$ $\cos\gamma=\frac{x^2+y^2-z^2}{2xy}=\frac{(a-b)^2\sqrt[3]{7a}-2(a-b)^7D^{-7}}{2((a-b)b\sqrt[3]{7a}+(a-b)^7D^{-7})};$](https://dxdy-01.korotkov.co.uk/f/c/7/c/c7ca8903d8cfdd2705d5ee42b506baa282.png)
Сейчас нужно подумать, на что сокращается дробь

Вот есть два числа

. Как найти их НОД? Его можно найти как НОД суммы и разности этих чисел, то есть НОД чисел

. Касаемо числа

можно сказать, что

в силу того, что исходное уравнение

либо

. Кто не понял, подробные пояснения под спойлером
(Оффтоп)
давайте сначала разберём, почему

Пусть

. Перепишем уравнение исходное в виде


.
Имеем противоречие. Для

принцип такой же!
Так как в силу леммы

, а также того факта, что

, который был показан в процессе доказательства леммы 1, дробь

сокращается на

. Осталось выразить

через

с помощью соотношений
![$[2.2]$ $[2.2]$](https://dxdy-01.korotkov.co.uk/f/0/d/e/0de769f831f4e3f65c522fdc7dc6ce7282.png)
и можно записывать

.
Получим
![$2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$ $2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$](https://dxdy-02.korotkov.co.uk/f/5/0/8/50810ba5f97a0f1da2e023ffe684957a82.png)
Оба числа

являются нечетными, так как число

после деления на двойку становится нечетным, а

и так ясно, что нечетное.
Можно ли выражение для

записать как-то иначе? Да, можно! Для этого берём и умножаем числитель и знаменатель дроби на два для удобства.
![$\cos\gamma=\frac{D^2\sqrt[3]{7a}F-2F^6}{2\sqrt[3]{7a}bD+2F^6};$ $\cos\gamma=\frac{D^2\sqrt[3]{7a}F-2F^6}{2\sqrt[3]{7a}bD+2F^6};$](https://dxdy-02.korotkov.co.uk/f/1/0/3/103742938259f4ea2a9c1608e04dce9c82.png)
Это новое выражение для

после приведения к ОБЩЕМУ знаменателю представляет из себя квадратное уравнение относительно

и этим нужно воспользоваться! Итак, после упрощения имеем
![$\sqrt[3]{7a}FD^2-2\sqrt[3]{7a}b\cos\gamma D-2F^6(\cos\gamma+1)=0;$ $\sqrt[3]{7a}FD^2-2\sqrt[3]{7a}b\cos\gamma D-2F^6(\cos\gamma+1)=0;$](https://dxdy-04.korotkov.co.uk/f/7/2/3/723b28271a69d1f9c58f5d4768e9a39382.png)
Решаем его как обычное квадратное уравнение, формируя Пифагорову тройку таким же образом, как в начале доказательства. Считаем дискриминант
![$\frac{D_3}{4}=(b\sqrt[3]{7a}\cos\gamma)^2+2F\sqrt[3]{7a}F^6(\cos\gamma+1)=\varepsilon_3^2;$ $\frac{D_3}{4}=(b\sqrt[3]{7a}\cos\gamma)^2+2F\sqrt[3]{7a}F^6(\cos\gamma+1)=\varepsilon_3^2;$](https://dxdy-04.korotkov.co.uk/f/3/6/1/361087138f57b375d572d6057f72484c82.png)
В равносильном виде он имеет вид
![$(b\sqrt[3]{7a}\cos\gamma)^2+2F\sqrt[3]{7a}F^6(\cos\gamma+1)-\varepsilon_3^2=0;$ $(b\sqrt[3]{7a}\cos\gamma)^2+2F\sqrt[3]{7a}F^6(\cos\gamma+1)-\varepsilon_3^2=0;$](https://dxdy-02.korotkov.co.uk/f/9/a/5/9a51b99f0131213b158cb686f84ab1ec82.png)
Получилось квадратное уравнение относительно
![$\sqrt[3]{7a}!$ $\sqrt[3]{7a}!$](https://dxdy-02.korotkov.co.uk/f/1/a/3/1a3acb59810c0b15c8eb268aa19f4d8e82.png)
Здесь надо отметить, что так как

, то у обоих квадратных уравнений произведение корней ОТРИЦАТЕЛЬНОЕ! А так как

, то корни берём с плюсом! Значит, считаем дискриминант квадратного уравнения относительно
![$\sqrt[3]{7a}$ $\sqrt[3]{7a}$](https://dxdy-01.korotkov.co.uk/f/8/5/1/85146eae9ed6ef328b50b39271a7bef382.png)
.
![$\frac{D_4}{4}=(F^7(\cos\gamma+1))^2+(b\cos\gamma)^2\varepsilon_3^2=(\varepsilon_4)^2;\eqno[5]$ $\frac{D_4}{4}=(F^7(\cos\gamma+1))^2+(b\cos\gamma)^2\varepsilon_3^2=(\varepsilon_4)^2;\eqno[5]$](https://dxdy-01.korotkov.co.uk/f/8/f/c/8fce38e02390e9aa3bdfa228c05ffae182.png)
Вот Пифагорова тройка готова. Осталось найти корни квадратных уравнений
![$D,\sqrt[3]{7a}$ $D,\sqrt[3]{7a}$](https://dxdy-03.korotkov.co.uk/f/6/8/1/681ec016eb5d3b8ff9de6c3e7bb3126082.png)
! Это просто уже
![$$\left\{
\begin{array}{lcl}
D=\frac{\sqrt[3]{7a}b\cos\gamma+\varepsilon_3}{\sqrt[3]{7a}F} \\
\sqrt[3]{7a}=\frac{-F^7(\cos\gamma+1)+\varepsilon_4}{(b_1\cos\gamma)^2}\\
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
\varepsilon_3=\sqrt[3]{7a}(FD-b\cos\gamma),\\
\varepsilon_4=(b\cos\gamma)^2\sqrt[3]{7a}+F^7(\cos\gamma+1) \ \eqno[6]\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
D=\frac{\sqrt[3]{7a}b\cos\gamma+\varepsilon_3}{\sqrt[3]{7a}F} \\
\sqrt[3]{7a}=\frac{-F^7(\cos\gamma+1)+\varepsilon_4}{(b_1\cos\gamma)^2}\\
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
\varepsilon_3=\sqrt[3]{7a}(FD-b\cos\gamma),\\
\varepsilon_4=(b\cos\gamma)^2\sqrt[3]{7a}+F^7(\cos\gamma+1) \ \eqno[6]\\
\end{array}
\right.$$](https://dxdy-01.korotkov.co.uk/f/8/2/a/82a0f42920252f168491cfb2e4c68c8f82.png)
Подставляем теперь соотношения для

в Пифагорову тройку пять.