А это зависит от того, что будет происходить на

. Может там еще какие-то элементы, у которых можно бесконечно брать прообраз, добавятся.
Если

то, по-моему, таких элементов быть не может.
Например, цепочка, которую мы вывели, базируется на функциях

В этой цепочке


обратим внимание на функцию

вблизи нуля:

дальше должно бы было быть

(что невозможно, так как

), если бы было условие

, но условие другое:

и потом

. Благодаря этому условию, функция

, дойдя до нуля, не прерывается, и благодаря этому условию, существуют функции

из которых функцией

можно бесконечное число раз брать прообраз от любого элемента

относительно функции

.
Теперь рассмотрим то, что происходит по теореме Кантора-Бернштейна. Имеем
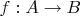
и

.
Обозначим через

элемент множества

и через

элемент множества

(что собой представляют

и

, было сказано уже много раз). Имеем цепочки

и

которые обе прерываются, потому что ни

не может отобразить

в какой бы то ни было

, ни

не может отобразить

в какой бы то ни было

.
Так что из этих функций невозможно построить такую функцию

, чтобы ею от элемента множества

или от элемента множества

можно было бесконечное число раз брать прообраз относительно функции

.
Других же функций здесь, по-моему, не предполагается.