Пытаюсь понять доказательство теоремы Кантора – Бернштейна в "НАЧАЛЕ ТЕОРИИ МНОЖЕСТВ" Н. К. Верещагина, А.Шеня
(
https://www.mccme.ru/free-books/shen/sh ... art1-2.pdf стр. 20 - 21).
Цитата:
Теорема 6 (Кантора – Бернштейна). Если множество

равномощно некоторому подмножеству множества

, а

равномощно некоторому подмножеству множества

, то множества

и

равномощны.
Доказательство. Пусть

равномощно подмножеству

множества

, а

равномощно подмножеству

множества

(см. рис. 2). При взаимно однозначном соответствии между

и

подмножество

переходит в некоторое подмножество

. При этом все три множества

и

равномощны, — и нужно доказать, что они равномощны множеству

, или, что то же самое,

.
Теперь мы можем забыть про множество

и его подмножества и доказывать такой факт:
если

и

равномощно

, то все три множества равномощны.
(Для единообразия мы пишем

вместо

.)
Пусть

— функция, осуществляющая взаимно однозначное соответствие

(элемент

соответствует элементу

). Когда

переходит в

, меньшее множество

переходит в какое-то множество

(см. рис. 3). Аналогичным образом само

переходит в некоторое множество

. При этом

, так как

.
Здесь, конечно, опечатка: не

, а

.
Цитата:
Продолжая эту конструкцию, мы получаем убывающую последовательность множеств

и взаимно однозначное соответствие

, при котором

соответствует

(иногда это записывают так:

). Формально можно описать
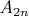
как множество тех элементов, которые получаются из какого-то элемента множества

после

-кратного применения функции

. Аналогичным образом
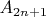
состоит из тех и только тех элементов, которые получаются из какого-то элемента множества

после

-кратного применения функции

.
Заметим, что пересечение всех множеств

вполне может быть непусто: оно состоит из тех элементов, у которых можно сколько угодно раз брать

-прообраз.
Теперь можно сказать так: множество

мы разбили на непересекающиеся слои

и на сердцевину

.
Я не понимаю, что собой представляет пересечение

всех множеств

. Этим пересечением не может быть ни одно из

, хотя бы потому что при отображении

ни одно из них не переходит в себя (по доказательству

переходит в себя).
Этим пересечением не может быть и ни один из слоев

, также хотя бы потому что при отображении

ни один из них не переходит в себя (более того, ни один элемент

не отображается в элемент, принадлежащий

).