Она даже в математике имеет специальное название.
см. в Википедии статью Гессиан функции
То, что в математике он имеет специальное название, я в курсе. Однако, меня тут попутал склероз и вместо фамилии Гессе я упомянул другую фамилию. Будем считать это опечаткой. Я думал, что в виду очень простого ответа задача имеет какой-то скрытый физический смысл, который позволит получить ответ без особых вычислений.
Тут я не понял. Допустим, мы хотим сначала усреднить по сфере, потом применить дифференциальный оператор

.
Э-э, нет. Я предполагаю, что дифференциальный оператор мы сначала уже подсчитали. Имея в виду некоторые соображения симметрии, ясно что внедиагональные элементы этого оператора нулевые. Также соображения симметрии наталкивают на мысль, что диагональные элементы его равны. Также соображения симметрии подсказывают, что этот оператор должен быть одинаковым для всех точек сферы ( а чем одна точка сферы лучше другой). И получается, что скорее всего оператор имеет вид

, где

- тождественный оператор. И тут не совсем очевидно, что
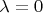
.
Но это не особо важно. (В конце концов это были лишь интуитивные догадки, которые нуждаются в обосновании). Важно, что этот оператор уже вычислен для всех точек сферы. И тут имеется две возможности. Первая. Применить этот оператор к некоторому произвольному диполю, который находится в центре сферы. Тем самым мы получим векторное поле на сфере, которое является напряжённостью на сфере электрического поля диполя. Вторая. Усреднить этот оператор по всей сфере. А затем его применить к тому же самому произвольному диполю. Опять же получим векторное поле на сфере.



