Arsh x через "длинный логарифм"

[e7e5]

Brukvalub писал(а):

1. Вам предлагали написать не ряд, а ф-лу Тейлора с остаточным членом в форме Лагранжа или Коши или еще какого-либо вида, позволяющего оценить величину этого ост. члена.

Уважаемый "Brukvalub", пожалуйста можно подробнее.
Вот например на MathWorld приводится формула (8) ряда Тейлора
http://mathworld.wolfram.com/InverseHyperbolicSine.html

Идейно понимаю таким образом: Если функция $f$ в некоторой точке $x_0$ представляется сходящимся степенным рядом, с какой-то областью сходимости, тогда можно найти коэффициенты ряда Тейлора, через производные этой функции.

Далее нужно выписать остаточнй член ряда ТЕйлора, как
$r_n(x)=f(x)-S_n(x)$
здесь $S_n(x)= \sum\limit_{k=0}^{n} \frac {f^k(x_0)} {k!} (x-x_0)^k$
PS Сижу с книжками и пытаюсь разобраться, any ideas& help are hihgly welcomed

[Brukvalub]

e7e5 в сообщении #156675 писал(а):

Далее нужно выписать остаточнй член ряда ТЕйлора, как
$r_n(x)=f(x)-S_n(x)$

Не совсем так. См. http://www.pm298.ru/tei.shtml, http://mathem.h1.ru/diff7.html, http://a-46.by.ru/2526.htm, http://ru.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0

[ewert]

Стандартный вид остаточного члена в форме Лагранжа:

$$r_n={f^{(n+1)}(\xi)\over (n+1)!}\cdot(x-x_0)^{n+1}$$

($\xi$ -- где-то между $x$ и $x_0$). Максимум производной часто легко оценивается явно, а если и не явно, то это даёт абстрактную оценку вида $O(h^{n+1})$, где $h=|x-x_0|$.

[GAA]

e7e5 писал(а):

Вот например на MathWorld приводится формула (8) ряда Тейлора
http://mathworld.wolfram.com/InverseHyperbolicSine.html
Идейно понимаю таким образом: Если функция $f$ в некоторой точке $x_0$ представляется сходящимся степенным рядом, с какой-то областью сходимости, тогда можно найти коэффициенты ряда Тейлора, через производные этой функции.

Говоря «Но на деле, для выписывания ряда достаточно знать соответствующие производные в нуле», я говорил о получении ряда Маклорена (ряда Тейлора по степеням $x$). Будем рассматривать положительные $x$. Для получения разложения «в бесконечности» (разложении по степеням $1/x$) удобнее почленно интегрировать разложение $1/\sqrt{1+x^2}$ по степеням $1/x$:

$$ \frac {1} {\sqrt{1+x^2}} = \frac {1} {x} \frac {1} {\sqrt{1+x^{-2}}} $$

,

$$ \frac {1} {\sqrt{1+x^{-2}}} = 1 + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n!} x^{-2n}$$

.
Cледовательно

$$1/\sqrt{1+x^2} = \frac {1} {x} + \sum_1^{\infty} (-1)^n \frac {(2n-1)!!} {2^n n!} x^{-2n-1}$$

.
Интегрируя почленно, получим

$$\int \frac {dx} {\sqrt{1+x^2}} = \ln{x} + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n! (-2n)} x^{-2n} + C$$

(*).
И т.к. $\ln(x + \sqrt{1+x^2}) \sim \ln{2x}$, при $x \to +\infty$ т.е. $\ln(x + \sqrt{1+x^2}) \sim \ln{2} + \ln{x}$, то устремляя почленно $x$ к $+\infty$ получим $C = \ln2$.

[ewert]

о хоссподи.

$${1\over\sqrt{1+x^2}}=(1+x^2)^{-1/2}=1+\left(-{1\over2}\right)x^2+{(-{1\over2})(-{3\over2})\over2!}x^4+{(-{1\over2})(-{3\over2})(-{5\over2})\over3!}x^6+\dots$$

и т.д. Стандартное разложение. К чему лирика?...

[GAA]

ewert писал(а):

о хоссподи.

$${1\over\sqrt{1+x^2}}=(1+x^2)^{-1/2}=1+\left(-{1\over2}\right)x^2+{(-{1\over2})(-{3\over2})\over2!}x^4+{(-{1\over2})(-{3\over2})(-{5\over2})\over3!}x^6+\dots$$

и т.д. Стандартное разложение. К чему лирика?...

И вместо $x$ подставить $1/x$?

Добавлено спустя 7 минут 36 секунд:

Было бы очень любезно с Вашей стороны, ewert, привести подробности.

[ewert]

да какие там ещё подробности, коли табличное разложение. И какие могут быть единицы на икс, коли разложение -- в окрестности нуля (не так ли?)

[GAA]

ewert писал(а):

И какие могут быть единицы на икс, коли разложение -- в окрестности нуля (не так ли?)

Нет, не так. На начало ноября 2008 года и в частности 09.11.08 номером (8) помечено разложение по степеням $1/x$:

Wolfram MathWorld писал(а):

$$\sinh^{-1} x = -\ln(x^{-1}) + \ln2 + \sum_{n=1}^{\infty} \frac{(-1)^{n-1}(2n-1)!!}{2n(2n!!)} x^{-2n} \qquad \qquad (7)$$

$$ =-\ln(x^{-1}) + \ln 2 + \frac {1}{4} x^{-2} - \frac {3}{32}x^{-4} + \frac {5}{96}x^{-6} - \dots \qquad \qquad \qquad (8)$$

В своем сообщении я цитирую вопрос e7e5, в котором указана именно формула (8), более того, я явно указываю: получаю разложение по степеням $1/x$. Получение разложения по степеням $x$ я обсудил во втором моем сообщении этой темы, и, так как e7e5 вопросы о нем не задал, к нему я больше не возвращался.

Добавлено на следующий день

Цитируя MathWorld, я допустил опечатку в расстановке скобок в знаменателе. Должно быть:

Wolfram MathWorld писал(а):

$$\sinh^{-1} x = -\ln(x^{-1}) + \ln2 + \sum_{n=1}^{\infty} \frac{(-1)^{n-1}(2n-1)!!}{2n(2n)!!} x^{-2n} \qquad \qquad (7)$$

$$ =-\ln(x^{-1}) + \ln 2 + \frac {1}{4} x^{-2} - \frac {3}{32}x^{-4} + \frac {5}{96}x^{-6} - \dots \qquad \qquad \qquad (8)$$

[ewert]

девятым-одиннадцатым-восьмым ничего здесь не помечено (да и странно бы), и уж вольфрамом -- тем более, и вообще странно обсуждать стандартные разложения. Вот есть они -- и всё.

[GAA]

ewert писал(а):

девятым-одиннадцатым-восьмым ничего здесь не помечено (да и странно бы), и уж вольфрамом -- тем более...

Здесь дана конкретная ссылка:

ранее в этой теме e7e5 писал(а):

Вот например на MathWorld приводится формула (8) ряда Тейлора http://mathworld.wolfram.com/InverseHyperbolicSine.html

Так как вопрос задан, и ссылку на MathWorld в этой теме дал я, то и отвечать, возможно, мне. Это я отчитался перед Вами, почему посмел выводить стандартное разложение.

ewert писал(а):

...и вообще странно обсуждать стандартные разложения. Вот есть они -- и всё.

Ваше замечание учел, и в дальнейшем стандартные разложения выводить не буду.

[ewert]

гыхм (это я уж от избытка чувств) а при чём тут ваще синусы, коли речь об ихних производных?...

[GAA]

ewert писал(а):

гыхм (это я уж от избытка чувств) а при чём тут ваще синусы, коли речь об ихних производных?...

Я не понял Вашего вопроса, но постараюсь быть вежливым в надежде на то, что Вы поможете мне на Форуме, если я обращусь с вопросом. Насколько я понимаю, разговор в теме шел о вычислении $\ln(x+\sqrt{1+x^2})$. Эта функция иногда обозначается как $\sinh^{-1}x$, или как $\mathop{\mathrm{arcsinh}}x$. Я выводил разложение этой функции для больших положительных значений аргумента.

[ewert]

ну а тут речь шла, как я понял, исключительно про малые. Ну да не суть, коли зайдёт когда-нибудь разговор по существу -- наверное, столкуемся

[e7e5]

GAA писал(а):

Будем рассматривать положительные $x$. Для получения разложения «в бесконечности» (разложении по степеням $1/x$) удобнее почленно интегрировать разложение $1/\sqrt{1+x^2}$ по степеням $1/x$:

$$ \frac {1} {\sqrt{1+x^2}} = \frac {1} {x} \frac {1} {\sqrt{1+x^{-2}}} $$

,

$$ \frac {1} {\sqrt{1+x^{-2}}} = 1 + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n!} x^{-2n}$$

.
Cледовательно

$$1/\sqrt{1+x^2} = \frac {1} {x} + \sum_1^{\infty} (-1)^n \frac {(2n-1)!!} {2^n n!} x^{-2n-1}$$

.
Интегрируя почленно, получим

$$\int \frac {dx} {\sqrt{1+x^2}} = \ln{x} + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n! (-2n)} x^{-2n} + C$$

(*).
И т.к. $\ln(x + \sqrt{1+x^2}) \sim \ln{2x}$, при $x \to +\infty$ т.е. $\ln(x + \sqrt{1+x^2}) \sim \ln{2} + \ln{x}$, то устремляя почленно $x$ к $+\infty$ получим $C = \ln2$.

Т.е Вы получили разложение функции $\ln(x + \sqrt{1+x^2})$, для больших положительных $x$

$$\int \frac {dx} {\sqrt{1+x^2}} = \ln{x} + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n! (-2n)} x^{-2n} + \ln2$$

(*).

Что -то запутался. Разве с рядом (8) на Mathworld сходится?
И я вроде тоже разложение для
$1/\sqrt{1+x^2} $ использовал, но сумма чуть другая получилась ( например нет

например $x^{-2n}$, но $x^{-2n}$, сравните пожалуйста.

И еще, если функцию заменили рядом, так все-таки, какаяя ошибка в вычислении ? Как ранее любезно заметел .Brukvalub, нужно эту ошибку оценить

[GAA]

e7e5 писал(а):

Т.е Вы получили разложение функции $\ln(x + \sqrt{1+x^2})$, для больших положительных $x$

$$\int \frac {dx} {\sqrt{1+x^2}} = \ln{x} + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n! (-2n)} x^{-2n} + \ln2$$

(*).

Не совсем так. Из (*) моего сообщения [это не совсем то, что у Вас] следует

$$\ln(x + \sqrt{1+x^2}) = \ln{x} + \sum_1^{\infty} (-1)^n \frac{(2n-1)!!}{2^n n! (-2n)} x^{-2n} + \ln2$$

,
что эквивалентно формуле (8) с MathWorld. [Цитируя MathWorld, я допустил опечатку в расстановке скобок: в знаменателе, конечно, должно быть $2n(2n)!!$]

e7e5 писал(а):

И я вроде тоже разложение для $1/\sqrt{1+x^2} $ использовал, но сумма чуть другая получилась ( например нет например $x^{-2n}$, но $x^{-2n}$, сравните пожалуйста.

Не понял, что Вы тут написали. Ранее Вы выводили разложение по степеням $x$ (разложение «для малых $x$», формула (5) на MathWorld).
[вставлено на следующий день утром]
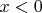
На первый взгляд можно поступить следующим образом. Т.к. функция $\ln(x+\sqrt{1 + x^2})$ нечетная, то при $x < 0$ можно вычислить $-\ln((-x)+\sqrt{1 + x^2})$. [Cводя тем самым задачу к вычислению функции от положительных значений аргумента.] Далее, при положительных $x$, если $x \le 1$ можно вычислять, используя разложение по степеням $x$ (разложение «для малых $x$»), а при $x > 1$ — используя разложение по степеням $1/x$ (разложение «для больших $x$»).
К сожалению, как я уже писал Выше, разложение по степеням $1/x$ содержит вычисление $\ln(x^{-1})$. Получаем «порочный круг». Как я и писал в этой теме выше, раз рассматриваемая функция выражается через стандартные элементарные функции: натуральный логарифм и квадратный корень, то для её вычисления следует воспользоваться алгоритмами вычисления этих функций. Метод извлечения квадратного корня изложен в примере 2 n3, §3, гл. 3 и Дополнении 2 «О скорости сходимости...» к этой же главе [4].
Метод вычисления натурального логарифма — в Дополнении к гл. 8 «Вычисление элементарных функций» [4].
Изложение этих вопросов в [4] немного неудачно. В изложении этих вопросов точно по-другому надо расставить ударения. Неудачная расстановка ударений, на мой взгляд, связана с тем, что книга посвящена не численным методам, а потому изложение в ней подчинено другой логике.

ref.
[4] Ильин В.А., Позняк Э.Г. Основы математического анализа. Т.1 — М.: Наука, 1982.
[/вставлено на следующий день утром]

e7e5 писал(а):

И еще, если функцию заменили рядом, так все-таки, какаяя ошибка в вычислении ? Как ранее любезно заметел .Brukvalub, нужно эту ошибку оценить

Brukvalub уже Вам ответил:

Brukvalub писал(а):

3. Если взять х таким, чтобы модуль общего члена ряда монотонно убывал, то ряд станет Лейбницевым. Для таких рядов ошибка замены суммы ряда на его частичную сумму не превосходит модуля первого из отброшенных членов.