Нобелевская премия 2022 года по физике

[Gickle]

Alex-Yu в сообщении #1567640 писал(а):

КХД -- это да. Но боюсь, что это как раз из нерешаемых. За исключением высокоэнергетического пертурбативного предела.

Я настроен гораздо более оптимистично. И разного рода непертурбативные методы не стоят на месте (функциональщина, "струнно-мотивированные" штуки, комплексный Ланжевен и т.п.), и эксперименты в ранее недоступных (в том числе численно) областях намечаются (та же NICA в Подмосковье), так что потихоньку-помаленьку, а данные копятся, уравнения пишутся, новые вещи понимаются.

Тут, разумеется, ещё вопрос, что понимать под "решить"/"не решить". Мне кажется, что многие вещи будут поняты в рамках "текущей парадигмы". Какие-то, наверное, лежат за пределами и требуют некоторого перосмысления (может, какое-то красивое переформулирование не в терминах калибровочных полей). А может, и действительно за пределами человеческих возможностей.

Alex-Yu в сообщении #1567640 писал(а):

Монте-Карло на решетке? Ну где ж такой компьютер взять, чтобы всерьез, а не обрывки...

Да даже будь большие компьютеры, вещи типа sign problem всю малину портят. Да и даже если помечтать, всё равно решёточные штуки они вик-повёрнутые, в основном про статику. Чтоб даже какие-нибудь партонные функции распределния из решёточной КХД достать, нужно прилично извертеться. Но люди же вертятся! :)

Да и, повторюсь, не одной решёткой же единой. Вон даже какие-то квантовые симуляторы калибровочных теорий (в основном на ультрахолодных атомах) потихоньку создают. Пока что там смехотворные вещи типа $1+1$ (недо-)КЭД, но кто знает, может, лет через N вместо огромных вычислительных центров можно будет на оптическую решётку нужных атомов накидать, кнопочку нажать и узнать ответ. Помечтать-то не вредно.

Osmiy в сообщении #1567574 писал(а):

Прям как теория БКШ.

Чем вас теория БКШ не устраивает-то? Как раз тот случай, когда и красиво, и ясную картину даёт, и приличные количественные результаты выдаёт.

[Osmiy]

Gickle в сообщении #1567692 писал(а):

Чем вас теория БКШ не устраивает-то? Как раз тот случай, когда и красиво, и ясную картину даёт, и приличные количественные результаты выдаёт.

У меня наоборот другие данные о БКШ сложились. Сначала все обрадовались ей, а потом оказалось, что она ничего толком не объясняет и не предсказывает количественно. Но я не настаиваю на этом. Это ИМХО так сказать.

[Anton_Peplov]

Alex-Yu
Насколько я понял Вашу мысль, все нерешенные задачи в физике делятся на два класса:
I) нерешаемые, потому что слишком сложные для коллективного разума физиков
II) нерешаемые, потому что требующие экспериментальных данных, которые никогда не будут доступны (пресловутый ускоритель размером с Галактику).

Разрешите задать Вам несколько вопросов:
- считаете ли Вы нерешаемой задачей построение термического уравнения состояния жидкости $p = p(V, T)$, пригодного для широкого класса жидкостей и имеющего какое-никакое теоретическое обоснование?
- построение нормально работающей теории турбулентных потоков - это задача уже решенная или недоступная коллективному разуму?
- верно ли, что про коллективные эффекты в плазме мы уже поняли всё, что можем понять?

Отдельные вопросы:
1. Можно ли надеяться на изобретение нового математического аппарата, который сделает решаемыми задачи, которые сейчас не решаемы? Вспоминается история, как Кардано несколько лет решал на геометрическом языке задачу о решении кубических уравнений, которую сейчас на алгебраическом языке может решить и школьник.
2. Можно ли надеяться на изобретение более эффективных способов ускорять частицы, чем гонять их по трубе в электромагнитном поле?

[Alex-Yu]

Gickle в сообщении #1567692 писал(а):

Вон даже какие-то квантовые симуляторы калибровочных теорий (в основном на ультрахолодных атомах) потихоньку создают.

А вот этого я не знал. Это реально круто. Если правда. Честно говоря, не понятно как это может быть. Как "перепрыгнуть" от КМ к КТП, от конечного к бесконечному числу степеней свободы. Опять решеточная аппроксимация? И что можно почитать об этом?

-- Вт окт 25, 2022 21:38:21 --

Anton_Peplov в сообщении #1567710 писал(а):

Разрешите задать Вам несколько вопросов:

Откуда ж мне знать ответы на ваши вопросы... Ну разве что турбулентность уже довольно успешно моделируется полностью (DNS). Но очень долго, мощности компьютеров пока маловато, но необходимая добавка мощности обозрима. Да и усредненный навье-стокс (RANS) работает нет так чтобы уж совсем плохо. Некоторое шаманство по обрыву цепочки уравнений Рейнольдса имеет место, но это работает. Это скорее решенная задача. Во всяком случае инженерам хватает.

Про новый матаппарат и новые методы ускорения -- скорее этого не будет никогда. Или, по меньшей мере, еще долго (столетия). Добавлю. Пример с Кардано несколько не в тему. Там была чисто математическая задача. А физика к математике не сводится.

А вообще мой пессимизм основан не на каких-то там умозрительных рассуждениях, в которые вы меня втянули, во всяком случае попытались :), а на прямом, даже в чем-то тупом наблюдении. Вот скажите, что действительно важного, концептуального произошло в физике с конца 80-х? А, по большому счету ничего :( Мелочи всякие делаются, не без того. Географы тоже чем-то там занимаются, диссертации пишут и т.п. Хотя эпоха великих географических открытий давно закончилась.

[Doctor Boom]

Alex-Yu в сообщении #1567716 писал(а):

А вообще мой пессимизм основан не на каких-то там умозрительных рассуждениях, в которые вы меня втянули, во всяком случае попытались :), а на прямом, даже в чем-то тупом наблюдении. Вот скажите, что действительно важного, концептуального произошло в физике с конца 80-х? А, по большому счету ничего :( Мелочи всякие делаются, не без того. Географы тоже чем-то там занимаются, диссертации пишут и т.п. Хотя эпоха великих географических открытий давно закончилась.

Вроде есть намек на новую физику

[Anton_Peplov]

Doctor Boom в сообщении #1567788 писал(а):

Вроде есть намек на новую физику

Намеков на новую физику со значимостью в две-три-четыре сигмы было уже пруд пруди, все как дым рассеялись при накоплении статистики. Увы, у СМИ есть дурная привычка трубить о таких результатах несоразмерно их значимости.

Интересны результаты в пять сигм и выше. О таких результатах было несколько заявлений, см. тему «Отклонения экспериментальных данных от Стандартной модели»

[chislo_avogadro]

Alex-Yu в сообщении #1567567 писал(а):

Беда нынче в том, что все наши теории ну уж слишком хороши.

Всё же есть два тёмных облачка, закрывающих примерно 95% неба.

И на каком масштабе там искать кажется тоже пока неизвестно.

[Gickle]

Извиняюсь за долгий ответ -- занят был.

Alex-Yu в сообщении #1567716 писал(а):

А вот этого я не знал. Это реально круто. Если правда. Честно говоря, не понятно как это может быть. Как "перепрыгнуть" от КМ к КТП. Опять решетка?

Да, решётка, разумеется. Строго говоря, попытка моделировать идёт именно что решёточные калибровочные теории. Насколько "реально", сами уж судите. :)

Я не специалист в этой области, если что, но общая идея примерно такая обычно вроде (на примере $U(1)$): операторам параллельного переноса и электрического и магнитного полей ставятся в соответствие операторы углового момента $L_z$, $L_{\pm}$. Для $l\to\infty$ это отображение работает идеально, а при конечных значениях $l$ -- только приближённо (операторы параллельного переноса не совсем унитарны $\implies$ получается усечённое гильбертво пространство). Дальше используется швингеровское представление углового момента в терминах бозоновских операторов ($a,b$), и складывается примерно такая картина: нужна оптическая решётка, в которой фермионы $c$ (ну или бозоны, если материя бозонная) будут жить в узлах, а в рёбрах между ними будут жить вот эти "швингеровские бозоны". В теории при этом вдобавок к интересующему gauge-matter члену типа $c^{\dagger} L_{+} c \sim c^{\dagger} b^{\dagger} a c$ будут и взаимодейсвтия типа 4-фермионных, нарушающих калибровочную инвариантность, но можно подобрать полные спины атомов $m_F$ так, чтобы только нужные слагаемые сохраняли полный спин.

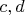
Дальше много всяких технических деталей: нужно обеспечить, чтобы бозоны "не прыгали" между рёбрами, для селекции члена $c^{\dagger} L_{+} c \sim c^{\dagger} b^{\dagger} a c$ по принципу сохранения спина нужно на самом деле два вида фермионов $c, d$ (поэтому на деле реализуются staggered фермионы) и т.п. Но сейчас экспериментаторы вроде как так научились ультрахолодные газы контролировать, что это вполне реально и осуществимо. Ну и вообще, как по мне, нобелевку-то больше за первые шаги в этой области (i.e., квантовых технологий) дали. Там, конечно, двое из трёх больше фотонщики, по-моему, но вот Zeilinger -- один из отцов-первопроходцев в области контроля ультрахолодных газов.

Вопрос того, насколько все приближения/допущения портят всю малину, до сих пор открыт и активно исследуется, как я понимаю. Может, в итоге станет понятно, что они "смертельны". Может, окажется, что более-менее серьёзные системы (неабелевы теории с материей в размерностях, отличных от $1+1$) технически реализовать практически невозможно, они не маштабируются и т.п. А может, появится альтернатива счёту решёточных моделей на суперкомпьютерах. Что было бы круто, конечно, потому что, как минимум, в этом подходе фермионы возникают естественным путём, так что никакой sign problem нет, а потому появилась бы возможность заглянуть в область существенно ненулевых значений хим. потенциала/фермионной плотности.

Цитата:

И что можно почитать об этом?

Список ниже не претендует на какую-то реперзентативность -- просто то, что у меня оказалось сохранённым во вкладках.

Что-то околообзорное, где можно дальнейшие ссылки найти:
1. M. Aidelsburger et al. Cold atoms meet lattice gauge theory. Phil. Trans. R. Soc. A 380, 20210064 (2021) // arXiv:2106.03063 [cond-mat.quant-gas]

Немного теории, тоже полуобзорного характера иной раз:
2. U.-J. Wiese. Ultracold quantum gases and lattice systems: quantum simulation of lattice gauge theories. Annalen Phys. 525, 777-796 (2013) // arXiv:1305.1602 [quant-ph]
3. E. Zohar, J.I. Cirac, B. Reznik. Quantum simulations of gauge theories with ultracold atoms: Local gauge invariance from angular-momentum conservation. Phys. Rev. A 88, 023617 (2013) // arXiv:1303.5040 [quant-ph]
4. D. González-Cuadra, E. Zohar, J.I. Cirac. Quantum simulation of the Abelian-Higgs lattice gauge theory with ultracold atoms. New J. Phys. 19, 063038 (2017) // arXiv:1702.05492 [quant-ph]
5. T. V. Zache et al. Quantum simulation of lattice gauge theories using Wilson fermions. Quantum Sci. Technol. 3 034010 (2018) // arXiv:1802.06704 [cond-mat.quant-gas]

Вариант конкретной экспериментальной реализации игрушечной модельки:
6. A. Mil et al. A scalable realization of local U(1) gauge invariance in cold atomic mixtures. Science 367, No. 6482, 1128-1130 (2020) // arXiv:1909.07641 [cond-mat.quant-gas]

[warlock66613]

Gickle в сообщении #1568481 писал(а):

попытка моделировать идёт именно что решёточные калибровочные теории

Но зато, как я понимаю, релятивистские, а не евклидовы, так?

[Alex-Yu]

warlock66613 в сообщении #1568493 писал(а):

Но зато, как я понимаю, релятивистские, а не евклидовы, так?

Я сразу подумал, что здесь естественным образом можно победить sign problem. В отличие от обычного компьютера. Впрочем, это только догадка, предположение.

[Gickle]

warlock66613 в сообщении #1568493 писал(а):

Gickle в сообщении #1568481 писал(а):

попытка моделировать идёт именно что решёточные калибровочные теории

Но зато, как я понимаю, релятивистские, а не евклидовы, так?

Да, хотя и в не совсем привычном обличии, поскольку в этих симуляторах в действительно реализуется гамильтонов подход. Если более точно, то на холодных атомах пытаются воспроизвести гамильтониан Когута-Сасскинда, ну а дальше уже готовят интересующее начальное состояние $\bra{\psi_0}$ и смотрят, как оно будет эволюционировать (повторяют эксперимент много раз, набирают статистику -- всё как у людей). В этом подходе штуки вроде лоренц-инвариантности менее явны, но на самом деле легко показать, что гамильтониан Когута-Сасскинда, как и полагается, лоренц-ковариантен (преобразуется как нулевая компонента вектора), так что всё по заветам релятивизма.