Всем привет, имеется вариационный ряд

, где

Нужно доказать, что

является сильно состоятельной то есть
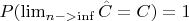
С одной стороны интуитивно ясно, что в пределе максимум будет равен правой границе равномерного распределения, но непонятно, как это формально доказать. Можете, пожалуйста, подсказать?