Свертка плотности вероятности с не-плотностью плотность?

[Divergence]

I) Ограничения:
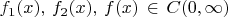
Пусть $f_1(x), \, f_2(x), \, f(x) \, \in \, C(0,\infty)$, где
$ f(x) \, := \, (f_1\, * \, f_2) \, := \, \int^x_0 f_1(x-u) \, f_2(u) \, du. $

II) Утверждения:
Утверждение 1: Если $f_1(x) \ge 0$ для всех $x>0$ и $f_2(x) \ge 0$ для всех $x>0$, тогда $f(x) \ge 0$ для всех $x>0$.
Утверждение 2: Если $f(x) \ge 0$ для всех $x>0$ и $f_2(x) \ge 0$ для всех $x>0$, тогда $f_1(x) \ge 0$ для всех $x>0$.
По-моему мнению, Утверждение 1 верно в силу определения интеграла.
По-моему Утверждение 2 неверно. Положительность $f(x)$ - это положительность интегральной суммы произведения функций, и из-за отрицательности $f_1(x)$ часть этой суммы может уйти в минус на небольшом интервале, не приводят к отрицательности всей интегральной суммы. Раз это неверно, то должны существовать примеры таких функций.
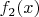
Утверждение 3: Известно, что если $f_1(x)$ и $f_2(x)$ это плотности гамма-распределений $f(x)$ тоже описывает плотность гамма-распределения.
стр.66-67 в Феллер В. Введение в теорию вероятностей и ее приложения. Том 2. (Мир, 1967):

$$f_1(x)=\frac{\lambda^a \, x^{a-1}}{\Gamma(a)} \, e^{- \lambda \, x} \quad f_2(x)=\frac{\lambda^b \, x^{b-1}}{\Gamma(b)} \, e^{- \lambda \, x} , \quad f(x)=\frac{\lambda^{a+b} \, x^{a+b-1}}{\Gamma(a+b)} \, e^{- \lambda \, x},$$

где $a>0$, $b>0$, $x>0$.

III) Вопрос: Пусть

$$f_1(x)=\frac{\lambda^a \, x^{a-1}}{\Gamma(a)} \, e^{- \lambda \, x}.$$

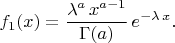
Можно ли привести пример функции $f_2(x) \in \, C(0,\infty)$ для которой
1) Условие $f_2(x) \ge 0$ для всех $x>0$ НЕ выполнялось, но при этом
2) $f(x) \, \in \, C(0,\infty)$ была бы плотностью вероятности, а именно $f(x) \ge 0$[/math] для всех $x>0$ и

$$\int^{\infty}_0 f(x) \, dx \, = \, 1$$