Нахождение функции Лагранжа плоского маятника

[htoya]

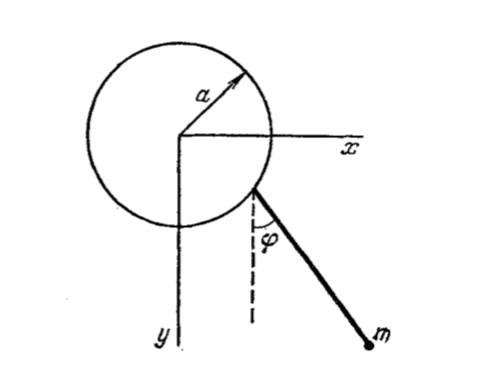
Задача из ЛандауЛифшица с приведенным решением оттуда же. Хотелось бы прояснить несколько моментов, которые я не поняла.

Найти функцию Лагранжа для плоского маятника, точка подвеса которого равномерно движется по вертикальной окружности с постоянной частотой $\gamma$ (рисунок выше)
Решение из книги:
Координаты точки $m$ :
$x = a \cos(\gamma t)+l \sin(\varphi)$
$y=-a \sin(\gamma t) + l \cos(\varphi)$
Функция Лагранжа:
$L = \dfrac{ml^2}{2}\dot{\varphi^2}+mla\gamma^2 \sin(\varphi - \gamma t)+ml \cos(\varphi)$
здесь опущены члены, зависящие только от времени, и исключена полная производная по времени от $mal\gamma \cos(\varphi - \gamma t)$.

Я пытаюсь проделать шаги, пропущенные в приведенном решении:
$\dot{x}=-a\gamma\sin(\gamma t)+l\dot{\varphi}\cos(\varphi)$
$\dot{y}=-a\gamma\cos(\gamma t)-l\dot{\varphi}\sin(\varphi)$
Потенциальная энергия $U=-mg(l\cos(\varphi)+a\sin(\gamma t))$

Составим функцию Лагранжа:
$L=\dfrac{m}{2}(l^2\dot\varphi^2\cos^2(\varphi)+a^2\gamma^2\sin^2(\gamma t)-2la\dot{\varphi}\gamma\cos(\varphi)\sin(\gamma t)+a^2\gamma^2\cos(\gamma t)+l^2\dot{\varphi^2}\sin^2(\varphi)+2la\dot{\varphi}\gamma\sin(\varphi)\cos(\gamma t))+mg(l\cos(\varphi)+a\sin(\gamma t))$

$L=\dfrac{m}{2}(l^2\dot{\varphi}^2+a^2{\gamma}^2+2la{\gamma}\dot{\varphi}\sin(\varphi - \gamma t))+mg(l\cos(\varphi)+a\sin(\gamma t))$

1)В решении написано, что члены, зависящие только от времени, опускаются. Значит убираем $mga \sin(\gamma t)$ и $a^2\gamma^2$. Но вот почему если они зависят только от времени, мы можем их убрать, это я не понимаю.

2)Почему во втором слагаемом в решении из книги $\gamma^2$ , а не просто $\gamma$. И почему нет $\dot{\varphi}$. Где я делаю ошибку?

3)Далее в решении написано, что исключена полная производная по времени от $mal \gamma \cos(\varphi - \gamma t)$. Это почти мое слагаемое из предыдущего вопроса, только опять же вторая степень все портит. И почему мы можем исключить его?

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- оставьте в виде картинки только собственно картинку, все остальное наберите как текст с формулами.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»

[zykov]

htoya в сообщении #1564170 писал(а):

Но вот почему если они зависят только от времени, мы можем их убрать, это я не понимаю.

А что будет с такими слагаемыми, если подставить Лагранжиан в уравнения Лагранжа — Эйлера?

htoya в сообщении #1564170 писал(а):

Почему во втором слагаемом в решении из книги $\gamma^2$ , а не просто $\gamma$. И почему нет $\dot{\varphi}$.

Да, так и получается, как у Вас.
Но дальше написано:

htoya в сообщении #1564170 писал(а):

исключена полная производная по времени от $mal \gamma \cos(\varphi - \gamma t)$.

$\frac{d}{dt}\left(mal \gamma \cos(\varphi - \gamma t)\right)=-mal \gamma (\dot\varphi - \gamma)\sin(\varphi - \gamma t)$.

htoya в сообщении #1564170 писал(а):

И почему мы можем исключить его?

https://dxdy.ru/post917386.html

[svv]

a) Должно быть $U=-mg(l\cos(\varphi){\color{magenta}-}a\sin(\gamma t))$. На конечный результат эта ошибка не влияет.

b) Вместо того чтобы исключать полную производную по времени, можно, наоборот, добавить к лагранжиану некоторую полную производную по времени. Идейно это то же, а психологически, возможно, проще:
Имеем неудобное слагаемое $mla\gamma\,\dot{\varphi}\sin(\varphi - \gamma t)$
Добавляем $\frac d{dt}\bigl(mla\gamma\cos(\varphi - \gamma t)\bigr)=-mla\gamma\,(\dot{\varphi}-\gamma)\sin(\varphi - \gamma t)$, которое его нейтрализует.
Получаем более простое $mla\gamma^2\sin(\varphi - \gamma t)$

с) Объяснение про полную производную есть и у Ландау-Лифшица, см. конец §2, стр. 13.

[htoya]

Спасибо всем!