Нюанс с законом Кулона-Амонтона

[reterty]

При выводе дифференциального уравнения, описывающего распределение вертикального давления в цилиндрическом сосуде, заполненном гранулированным материалом, возникает ситуация, когда сила трения покоя молчаливо заменяется своим максимальным значением без каких-либо аргументированных доводов.
Рассмотрим цилиндрический контейнер радиусом $r$, заполненный гранулированным материалом с плотностью $\rho$.

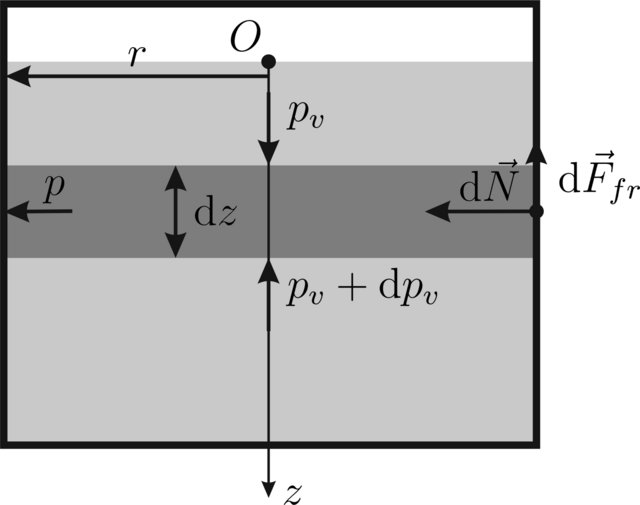
Глубину столба (координата $z$) будем отсчитывать от верхней свободной поверхности. Выделим в столбе инфинитезимальный слой толщиной $dz$ между $z$ и $z+dz$. Тогда вертикальными силами, действующими на этот слой вниз будут сила давления $p_v\pi r^2$ и сила тяжести слоя $dm g=\rho g \pi r^2 dz $. Вертикально вверх действует сила давления $(p_v+dp_v)\pi r^2$ и сила трения покоя $dF$. Согласно гипотезе Янссена вертикальное давление в гранулированных материалах частично передается и в горизонтальном направлении: $p=kp_v$, где $k$- коэффициент пропорциональности. Тогда силу трения можно расписать следующим образом: $dF=\mu dN=\mu p 2\pi r dz=2k\mu p_v\pi r dz$. Используя уравнение равновесия слоя, получаем следующее дифференциальное уравнение:

$$\frac{dp_v}{dz}=\rho g-2k\mu \frac{p_v}{r}$$

Так вот, в этом выводе мне не понятна замена силы трения покоя ее максимальным значением. Глядя на последнее уравнение можно думать что такая замена минимизирует скорость прироста давления с глубиной а следовательно минимизирует общую энергию деформации столба гранулированного материала. Но это лишь моя догадка.....

[svv]

reterty в сообщении #1564035 писал(а):

не понятна замена силы трения покоя ее максимальным значением

Это тоже одна из гипотез, на которой основывается модель. См. статью Modèle de Janssen во французской Википедии, пункт Hypothèses, гипотеза 2.
Но Вы, действительно, предлагаете хорошее обоснование — минимальность энергии деформации.
Похоже на статически неопределимые системы в статике (а может, это оно и есть), где для разрешения неопределённости приходится привлекать теорию упругости.

[sergey zhukov]

reterty
Похожая задача, но попроще:

Возьмем длинный брусок определенного веса, который толкают горизонтальной силой по горизонтальной поверхности (но он неподвижен из-за трения). Каждый вертикальный слой бруска удерживается на месте силой трения (эпюра касательного напряжения по длине бруска) и давлением следующего слоя (эпюра давления по длине бруска). В рамках абсолютно твердого тела (пока брусок неподвижен) есть множество решений для этих эпюр, т.е. решение неоднозначно.

Можно предположить, что эпюра касательных напряжений равномерно распределена по всей длине бруска. Тогда эпюра давления будет линейно падать от максимума в начале бруска до нуля - в конце бруска. Если горизонтальную силу наращивать, то эпюра касательных напряжений будет одновременно расти по всей длине бруска, пока всюду не дорастет до максимального значения и брусок не сдвинется.

Можно предположить, что все трение максимально сосредоточено в самых ближних к приложенной силе слоях. Тогда эпюра касательного напряжения имеет максимально возможное значение от начала бруска до некоторого процента его длины, а дальше по длине равна нулю. Эпюра давления опять линейно падает от максимума до нуля на участке, где эпюра касательного напряжения имеет максимальное значение. Если горизонтальную силу увеличивать, то участок максимальной эпюры касательных напряжений удлинняется, пока не захватит весь брусок и он не сдвинется.

По моему, однозначное решение получается, если выбрать модель упругого тела в виде чередующихся абсолютно твердых слоев, связанных пружинами. В этом случае очевидно, что правильным будет второе решение, особенно, если предположить произвольно медленное увеличение приложенной силы. Ясно, что в этом случае слои, близкие к точке приложения силы, должны перемещаться, т.е. сила трения для них должна иметь максимальное значение. Те слои, которые пока не перемещаются, не будут передавать давление дальше, пока не сдвинутся. Этот же вариант соответствует минимальной энергии деформации, т.к. перемещение точки приложения силы до достижения равновесия будет тут минимальным.