3. Теперь покажем, как построить форму

для неотрицательных на

многочленов на примере многочлена Моцкина

Итак, будем строить форму
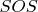
для многочлена

. Как показано в п.1. достаточно построить формы

для многочленов

. Поскольку

то достаточно построить форму

лишь для

. Для этого, как показано в п.2. достаточно построить формы

для многочленов

:
3.1. Для многочлена

требуемая форма строится обратными подстановками непосредственно из рациональной функции

, поскольку она не имеет отрицательных коэффициентов:






3.2. Для многочлена

требуемая форма строится обратными подстановками непосредственно из многочлена

, поскольку он не имеет отрицательных коэффициентов:






3.3. Ввиду симметрии

, для многочленов

достаточно построить требуемую форму только для одного из них, пускай это будет

. В отличие от 3.1 и 3.2 попытка получить многочлен с неотрицательными коэффициентами подстановкой

не удастся. Поступим следующим образом: разрежем квадрат

на две области прямой

. Область

разрежем на две области прямой

. Получим три области (Рис.1):
I -

,
II -

,
III -

.
Дальнейшая идея в следующем: построить для каждой из областей некоторую свою форму

и склеить все в требуемую форму.
3.3.1 Для I -й области имеем:


3.3.2 Для II -й области имеем:




3.3.3 Для III-й области будет продемонстрирована идея, дающая гарантированное построение формы. (в предыдущих случаях 3.3.1, 3.3.2 текущая идея не применялась, поскольку мне хотелось показать её для области, где непосредственные подстановки не сработают - а это, как и следовало ожидать от многочленов - окрестности корней как самого многочлена, так и его производных)
Итак, непосредственная подстановка для III-й области:

не срабатывает. Пусть

. Для всех

рассмотрим кривые

, заданные уравнениями

при

(Рис.1 синий цвет) и

(Рис.1 зеленый цвет). В III-область попали лишь кривые, заданные уравнениями с
. Проведем рациональную кривую

так, чтобы для

выполнялось

. В данном случае достаточно

(разложили

в ряд Тейлора в точке

до 3-й производной и взяли среднее). Теперь, по
Теореме 3.1 многочлен

не имеет на

отрицательных коэффициентов. Это означает, что каждый его коэффициент может быть представлен формой

, поэтому он сам (а следовательно и

) представляется формой

. Точно так же, по
Теореме 3.1, многочлен

не имеет на

отрицательных коэффициентов, поэтому он сам (а следовательно и

) представляется формой

. Итак:




.
Т.о. для III-й области произведена склейка по рациональной кривой

.
3.4 осталось склеить формы I- и III-области по прямой

а затем получившуюся форму с формой II-области по прямой

.
В п.3.3.3 реализована следующая идея:
Рассматриваем многочлен двух переменных

как многочлен одной переменной

с коэффициентами - многочленами от

. Тогда, если мы отметим на плоскости все линии

, то к любой области плоскости, не содержащей внутри себя этих линий или их частей (однако, и это важно, граница такой области может являться частью линий

), можно применить
Теорему 3.1. Т.е. если кусок плоскости, ограниченный линиями

, где

, а

- рациональные функции, не содержит внутри своей границы частей линий

, то многочлен

не имеет отрицательных коэффициентов на

.
Т.о. если удастся разрезать единичную область рациональными линиями на области, не содержащие линий нулей производных, то удастся и построить нужную форму для этой единичной области. Проблема в том, что в общем случае функции

заданные уравнениями

не являются рациональными. Поэтому (как в примере), поступаем следующим образом:
- домножаем многочлен

на некоторый многочлен

, где

- неотрицательный параметр:

- путем "шевеления" параметра, добиваемся "шевеления" линий нулей производных

(на Рис.1 это синяя и зеленая линии, при значении параметра

и

соответственно)
- проводим между этими линиями некоторую рациональную линию (на Рис.1 это

), которая разрежет нашу область на две (обозначим их по параметрам линий, в них содержащихся

).
- для области

применяем
Теорему 3.1 к многочлену

- для области
применяем
Теорему 3.1 к многочлену

- склеиваем получившиеся формы по рациональной линии.
(Оффтоп)
Думаю, стоит описать эту схему, примененную более чем к одной линии нулей производных, проходящих через корень многочлена, подробно в следующих сообщениях.
Данную процедуру (с некоторыми уточнениями, о которых позже) можно применять для любой достаточно малой окрестности любой точки единичного квадрата в том случае, если линии нулей производных не являются корнями многочлена, т.к. в этом случае "пошевелить" их путем "шевеления" параметра не получится. Однако для многочлена двух переменных это не проблема, т.к. если

то

, где

- неотрицательный многочлен, обнуляемый лишь конечным числом точек. Ну а в окрестности каждой такой точки процедура применима для такого многочлена

, а значит он представим формой
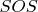
.



