Не могу разобраться как победить этот последний минус. Хотя если записать это уравнение относительно центра масс, то все становится хорошо. Но принцип не дает так просто отвернуться и не понять, в чем, собственно, соль проблемы)
Чтобы понять, в чём проблема, я предлагаю Вам разрешить парадокс.
Примем два упрощающих предположения:
1) Пренебрегаем моментами импульса вращающихся колёс (как и Мещерский).
2) Будем считать, что вся масса системы "велосипедист+велосипед" сосредоточена в центре масс. Отсюда, кстати, следует и 1).
Пусть велосипедист ездит по кругу, вращаясь вокруг прямой

. Точка

находится на земле, а

находится на той же высоте, что и центр масс (с учётом наклона велосипедиста). Колесо касается земли в точке

, центр масс в точке

.
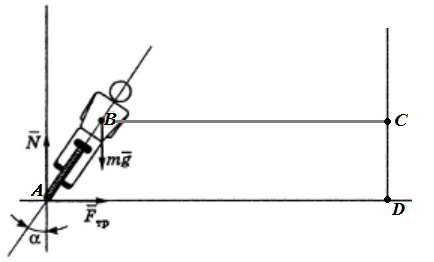
Я хочу вычислить суммарный момент всех сил, действующих на систему, относительно точки

. Момент силы — величина векторная, но меня интересует только проекция вектора момента на ось,
перпендикулярную рисунку. Если эта ось, проходя через

, направлена к "зрителю", то моменты силы тяжести и силы трения будут положительными (они стремятся вращать велосипедиста вокруг

в плоскости рисунка против часовой стрелки). А момент силы реакции опоры будет отрицательным (стремится вращать велосипедиста вокруг

в плоскости рисунка по часовой стрелке). Находим
момент силы тяжести:

момент силы трения:

момент силы реакции:

Поскольку момент импульса относительно точки

сохраняется, сумма этих моментов сил равна нулю. Отсюда находим

. Всё прекрасно!
Теперь найдём то же самое относительно точки

.
момент силы тяжести:

момент силы трения равен нулю, потому что плечо равно нулю
момент силы реакции:

Из условия равенства суммарного момента нулю находим

— явно неверный результат.
В чём дело?
Если аналогично найти сумму моментов относительно точки

(это
неподвижная точка, мгновенно совпадающая с точкой касания колёс и земли), получим, что и момент силы трения, и момент силы реакции равны нулю (т.к. равны нулю радиус-векторы точек приложения этих сил относительно

). Как Вы помните, нет никакой дополнительной центростремительной силы. Остаётся момент силы тяжести

. Приравнивая сумму к нулю, получаем опять

.
В чём же дело?



