А в момент представленный на рисунке, ускорение тоже параллельно оси X?
Я Вас не очень понял по нескольким причинам:
1) Желательно уточнить, говорите ли Вы об угловом ускорении

, или о линейном (обычно обозначается

, но у Фомичёва

или

, из видео непонятно). Предположу, что об

.
2) Я не говорил, что при движении в плоскости

вектор

параллелен оси

. Я говорил, что он параллелен оси

(сюда включается и случай нулевого

). Поэтому мне непонятен смысл слова «тоже» в цитате.
3) Фомичёв рассматривал случай твёрдого тела или нескольких твёрдых тел (каждое из звеньев — твёрдый стержень). При движении твёрдого тела угловая скорость

и её производная = угловое ускорение

определяются однозначно. Вы же в последнем примере рассматриваете движение точки. В этом случае можно ввести понятие угловой скорости относительно центра, но это уже немного другая штука, и она зависит от выбора центра. Например, если в ситуации на картинке неподвижный центр находится в точке

, то в данный момент

, а если в

, то нет.
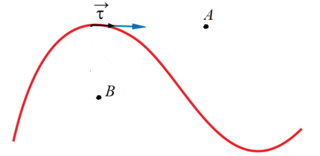
Аналогично и угловое ускорение зависит от выбора центра. Представьте, что в парке детский паровозик равномерно движется по окружности. Человек, наблюдающий за его движением из центра окружности, должен поворачивать голову равномерно, т.е. угловое ускорение равно нулю. Человек, наблюдающий за паровозиком издалека, поворачивает голову то вправо, то влево.
В общем, Вы видите, что это другая ситуация, и сейчас давайте рассматривать движение твёрдого тела, а не одной точки.
Просто, как я уже писал,


— правильно.

— правильно.

— неправильно. Вместо этого

, потому что угловая скорость сохраняет направление (перпендикулярное к плоскости движения). То есть Вы отбросили первое слагаемое, а надо было второе.
Я догадываюсь, почему Вы подумали, что

. Потому что в начальный момент

, а последняя постоянна. Но ведь это только в начальный момент! А далее равенство нарушается, и

совсем не константа, она даже знак меняет.



