Huz, а Вы можете запостить здесь Ваш исходный код на C(++) для самого простого случая? Например, для 12 делителей.
My code is more general than that. The primary tool I've been using is the perl program
oul ("oneseq upper limit"). When targetting T(n/2, k), the first levels of recursion are for primes

via the
forcep function, which iterates over all sets of powers

for each element; the remaining levels of recursion occur via the
recurse function, which first decides which element to target next, then iterates over available powers, within which it iterates over primes

.
Each level of recursion assigns a prime power to some element, where the product of assignments to element
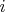
is stored as

; the main
recurse function concentrates on satisfying the highest odd prime dividing

. When there are no more odd factors to satisfy in any element (or in some cases earlier), the recursion terminates with a call to the
walk_v function.
There are special cases for walking those cases where some

, or where one or more

, but the core case loops over this:
Код:
if (all { gcd($o[$_], $q[$_]) == 1 } 0 .. $k - 1) {
if ($print) {
print STDERR $o[0] * $q[0], "\n";
} else {
return $o[0] * $q[0] if all { is_tau($o[$_], $t[$_] } 0 .. $k - 1;
}
}
In similar fashion to dmitry40's code, we have

as the product of allocated prime powers for each

,

,

,

calculated by
CRT,

. So for each

we check first via gcd() that we will not supply a higher power of any fixed prime, then check whether

for all
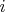
.
The
$print option in the above is there for those cases where the values are too large to factorize in the order we encounter them, such as for T(46,7). In this case I can print out all the candidates, then separately sort them and check in ascending order (using code that I have not yet tested).
If you'd like more information about specific parts of the code, feel free to ask more specific questions. :)
-- 07.06.2022, 22:51 --That is supposed to say "

= lcm(...)", not sure how to make it say that.