Неожиданно, удалось доказать, что существует максимум конечное количество четвёрок последовательных натуральных чисел, имеющих

делителей (

фиксированное простое число,

натуральное).
Доказательство начнём с двух лемм.
Лемма 1. Пусть

имеет

делителей,

- простой делитель

, входящий в его разложении на простые в степени
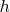
. Тогда либо

, либо

, либо

(причём, простой делитель делитель первого и третьего типов может быть только один).
Заметим также, что

делится на

. Это будет использовано в доказательстве второй леммы.
Лемма 2. Пусть

имеет

делителей. Тогда

можно представить в одном из следующих видов (

натуральные,
 простое
простое):
1)

2)

3)
 Доказательство.
Доказательство. В разложении

на простые множители либо есть простое в первой степени, либо нет. В первом случае

имеет вид 2). Во втором случае в разложении

на простые либо есть простые в степени кратной

, либо нет. В первом случае

имеет вид 3), а во втором

имеет вид 1).
Теперь перейдём к доказательству основного утверждения. Среди четырёх последовательных натуральных чисел, имеющих

делителей есть два чётных. Обозначим их
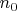
и
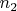
, так что

и

. Тогда

. Заметим, что
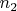
принадлежит второму типу, то есть

. Далее будут рассмотрены три случая в зависимости от того, к какому из трёх типов принадлежит
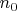
.
I.

. Подставив в уравнение

, получим

, что невозможно, так как в левой части разность квадратов.
II.

,

нечётное. Подставив в уравнение

, получим

НОД сомножителей в левой части равен двум, поэтому один из них имеет вид

либо

. Тогда

или

. Второе уравнение неразрешимо по теореме Михэйлеску, а первое является уравнением Туэ степени

, которое имеет конечное количество решений.
III.

или

. В первом случае получаем уравнение

, которое неразрешимо, так как слева разность квадратов. Рассмотрение второго случая аналогично разбору случая II. (уравнение Туэ получается то же самое).
-- 27.05.2022, 16:12 --Оформить доказательство было сложнее, чем придумать.
