Попробую всё же доказать неразрешимость стартового уравнения для

некратного пяти. Имеем на числовой оси три точки

равноудаленные (последовательно) на расстоянии

Одно из чисел делится на

, причем ровно одно, поэтому тройка (чтобы

оказалось квадратом) должна быть в четной степени. Точно так же любое простое

может входить в каноническое разложение множителей

только в четной степени, единственное исключение — число
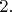
Если

четное, то остальные множители нечетные, тогда и двойка должна быть в четной степени. В этом случае имеем три квадрата, но единственные квадраты на расстоянии

это

которые не подходят. Последняя возможность:

нечетное при четных

В одно из них двойка входит в

-й степени, значит и во второе должна входить в нечетной степени, то есть

— удвоенные квадраты.

Только так:

Но между ними лежит число

, которое квадратом не является. Значит

не квадрат.
Для множителей кратных пяти, думаю, можно доказать подобными методами, что никакое простое

не может делить

А это на виду:

И хорошо согласуется с отсутствием иного решения биквадратного Пелля. Кроме того, вопросы разрешимости подобных уравнений точно уж за гранями школьной программы.



