Я всегда придерживался такой терминологии:
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
— отрезок (оба конца включаются);
![$(a,b]$ $(a,b]$](https://dxdy-01.korotkov.co.uk/f/c/6/f/c6f523011785edb445cc341039ecd26e82.png)
или

— полуинтервал (один конец включается, другой — нет);

— интервал (ни один конец не включается).
Термин "промежуток" обозначает любой из четырёх перечисленных вариантов.
По-моему, в ЕГЭ эти термины употребляются так же. Или я чего-то не заметил?
Что касается промежутков возрастания и убывания, то здесь всё однозначно следует из определений возрастающей и убывающей функции. В этом определении производная вообще не упоминается, поэтому не нужно интересоваться, существует ли производная и равна ли она нулю.
Функция

является возрастающей на всей числовой оси, в том числе и в точке

.
Функция

является убывающей на промежутке
![$(-\infty,0]$ $(-\infty,0]$](https://dxdy-01.korotkov.co.uk/f/c/8/8/c889590104be3ba29df8e0f77d56213e82.png)
и возрастающей на промежутке

. В точке

эта функция не является ни возрастающей, ни убывающей, но это не мешает включать эту точку в оба промежутка.
Ещё забавнее функция

Она возрастает в точке

, при этом ни на каком промежутке вида
![$(-\varepsilon,0]$ $(-\varepsilon,0]$](https://dxdy-04.korotkov.co.uk/f/7/b/a/7ba884eafb29633827869d136f63556082.png)
или

,

, она возрастающей не является.
Вложение:
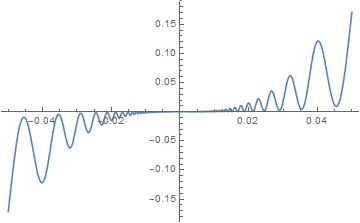 Grh.gif [ 4.52 Кб | Просмотров: 1741 ]
Grh.gif [ 4.52 Кб | Просмотров: 1741 ]



