Откуда

По-моему, получаются разные расстояния от этой точки до вершин треугольника.
Благодарю, что заметили. Да, я в решении ошибся в нескольких местах. Верное решение следующее.
Обозначим точки из условия:

,

и

Найдём уравнение плоскости, проходящей через точки

:


Найдём уравнение плоскости

, перпендикулярной вектору
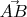
и проходящую через середину отрезка

. Направляющий вектор плоскости

:

Условие принадлежности середины

плоскости

:

Аналогично найдём уравнение плоскости

, перпендикулярной вектору

и проходящую через середину
отрезка

.

Условие принадлежности середины

плоскости

:

В итоге, точка центра окружности находится из решения системы уравнений:

Единственным решением этой системы является точка:

. Можно убедиться, что расстояние от этой точки до точек

,

,

равно

.
-- 22.05.2022, 19:05 --Посмотрите на своё первое сообщение:
Поэтому проведём две прямые, каждая из которых:
- перпендикулярна одной из сторон треугольника
- лежит в плоскости трёх точек треугольника
Где здесь сказано, что прямые должны проходить через середины сторон треугольника?
Точно. Благодарю!
Вот страсти какие…
Есть у нас треугольник

. Находим вектор

, перпендикулярный вектору

, и пишем уравнение прямой, проходящей через середину отрезка

. Далее находим вектор

, перпендикулярный вектору

, и пишем уравнение прямой, проходящей через середину отрезка

. Остаётся только найти точку пересечения.
Подумав, каким уравнением лучше задать прямую, проходящую через середину отрезка AC, в итоге остановился на таком решении.
Вашу задачу можно решать многими способами. Вы же изучаете курс аналитической геометрии? Я имел в виду следующее.
В курсе аналитической геометрии изучается много чего, и в частности — скалярное произведение векторов и условие ортогональности (перпендикулярности, если они ненулевые) векторов:

и

ортогональны тогда и только тогда, когда

. Пользуясь условием ортогональности векторов, получаем для

и

уравнения

и

, откуда находим

и

, а затем векторы

и

. Далее находим середины отрезков

и

. Имея точку (середину отрезка) и направляющий вектор (

или

), перпендикулярный соответствующему отрезку, составляем уравнение серединного перпендикуляра (каноническое или параметрическое; в последнем случае параметры нужно обозначить разными буквами). Эти уравнения объединяем в одну систему и находим точку пересечения.
Я не утверждаю, что это решение самое короткое, но оно прямо соответствует утверждению "центр описанной окружности треугольника является точкой пересечения серединных перпендикуляров к его сторонам".
Благодарю вас за полезную учебную рекомендацию!
Решение получилось следующее.





Аналогично получим, что

.
Так как

и

, то

и

.
Середина отрезка

имеет координаты:

. Середина отрезка

имеет координаты:

.
---
Решение, используя каноническое уравнение прямой.
Каноническое уравнение прямой с направляющим вектором

и проходящей через середину

:

Каноническое уравнение прямой с направляющим вектором

и проходящей через середину

:

Далее необходимо решить систему уравнений:

Единственным решением этой системы является точка:

. Можно убедиться, что расстояние от этой точки до точек

,

,

равно

.
---
Решение, используя параметрическое уравнение прямой.
Составим уравнения прямых:
-

с направляющим вектором

и проходящей через середину

.
-

с направляющим вектором

и проходящей через середину

.


Ответом будет решение системы из трёх уравнений относительно параметров

и

, отражающее условие пересечения прямых

и

:

Единственное решение:

.
Подставим значение любого из найденных параметров в соответствующее уравнение прямой и найдём, что точкой пересечения является точка:

. Можно убедиться, что расстояние от этой точки до точек

,

,

равно

.



