Дискретное преобразование Фурье на MATLAB

[Kevsh]

Здравствуйте, для начала хотелось бы спросить кое-что по данному выводу:

Вывод о том, что частота дискретизации должна превышать 2 частоты входного сигнала мне совершенно непонятен. Я понимаю, что нужно сделать так, чтобы функцию можно было бы восстановить только одним образом, то есть не должно существовать $m$, но причём тут частота никак не пойму. Вот откуда берётся это "0.5"?
После этого доказательства вводится дискретное преобразование Фурье: $\dot X(n)=\frac1 N \sum\limits_{k=0}^{N-1}x(k)e^{-j\frac{2\pi n}{N}k}$, вот его работу я хотел проверить с помощью MatLab. Я написал следующий код:

clear;
N=16;
f0=50;
fs=400;
x=(0:N-1);
y=2*sin(2*pi*f0*x/fs)+sin(6*pi*f0*x/fs+pi/4);
y_fft=fft(y, N);
y_myft=zeros(16);
for n=0:N-1
    for k=0:N-1
        y_myft(n+1)=y_myft(n+1)+y(n+1)*exp(-1j*2*pi*n*k/N);
    end
end
y_myft=y_myft/N;
figure;
grid on;
hold on;
plot(x, abs(y_myft), 'bo');
title('my FT')

Что-то вообще ничего не выходит, а ошибки я не вижу. При этом преобразование с помощью встроенной функции fft отлично работает. Получается, что я не до конца понимаю работу этого преобразования, в чём может быть ошибка? Моя идея была в том, чтобы в ячейке с номером $N$ лежала сумма с участием $n=N-1$.

[svv]

Пусть $f_0 \in (0,\frac {f_s}2), \;f=f_s-f_0$, тогда $f\in (\frac {f_s}2, f_s)$.
Покажите, что гармонический сигнал с частотой $f$ неотличим от некоторого гармонического сигнала с частотой $f_0$ по значениям в моменты времени $t=kt_s$.
Это — ещё одна причина неоднозначности, о которой авторы не написали. Она и накладывает ещё вдвое более жёсткие ограничения на спектр сигнала, если мы всё же хотим однозначности.

-- Сб апр 16, 2022 23:51:03 --

Kevsh в сообщении #1552752 писал(а):

Я понимаю, что нужно сделать так, чтобы функцию можно было бы восстановить только одним образом, то есть не должно существовать $m$, но причём тут частота никак не пойму.

Как Вы неудачно выразились. Можно подумать, что наличие или отсутствие $m$ — это свойство гармонического сигнала, и хорош тот сигнал, у которого $m$ нет. (А как это определить?)
На самом деле берутся два сигнала вида $\sin 2\pi f t$ с частотами, отличающимися на $mf_s$, где $m$ целое. Например, при $m=1$ их частоты отличаются на $f_s$. И у таких сигналов значения в моменты времени $kt_s$ совпадают.

[Евгений Машеров]

Никогда не замечали, как в кино вдруг начинают вертеться в обратную сторону колёса автомобилей и карет? Вот как раз частота вращения колеса превысила половину частоты кадров. Какая-нибудь отметина на колесе от одного кадра к следующему успевает пройти больше пол-оборота, что воспринимается, как поворот менее чем на пол-оборота, но в обратную сторону. А если колесо успеет сделать 2, 3 и более, любое целое число оборотов, оно будет казаться неподвижным.
Кстати, в приведенном Вами тексте некоторое упрощение. Хотя чаще всего действительно интересуются частотами от нуля до половины частоты квантования (частоты Найквиста-Котельникова-Шеннона, встречаются все мыслимые комбинации имён), принципиальное ограничение - ширина полосы не более половины частоты квантования. Однажды возникла задача на основе данных радиотермометрии оценить пульсовые колебания кровотока в мозге. Только прибор выдавал данные раз в полторы секунды (0.7 Гц), а частота пульса обычно лежит в пределах 60-90 в минуту (1-1.5 Гц). Получилось, но если бы были в сигнале компоненты, лежащие вне оцениваемой нами полосы, они бы наложились на сигнал и отделить бы их было бы невозможно.

[Евгений Машеров]

А что не совпадает? Что ожидали, что получили?

[Kevsh]

Евгений Машеров
Ошибка была в одном символе в 11 строке, нужно было так:

y_myft(n+1)=y_myft(n+1)+y(k+1)*exp(-1j*2*pi*n*k/N);

Отловил очень просто: при $n = 0$ сумма должна равняться просто сумме значений функции во всех 16 точках, а в итоге суммировалось 1-е значение 16 раз, вот и выводился какой-то бред. Если добавить это исправление, то результат совпадает со встроенной функцией fft. Ваш пример с колесом в принципе показывает, как мне кажется, в чём вообще проблема. Однако ну никак не пойму, как это аналитически понять – ну вот есть у нас это равенство $\sin(2\pi f_0 k t_s )=\sin(2\pi (f_0 + mf_s)k t_s)$. Допустим, у нас всё плохо и $f_0=0,7f_s$, тогда получаем $\sin(2\pi f_0 k t_s )=\sin(2\pi f_s(0,7 + m)k t_s)$, ну и что ? Заменю на $f_0=0,2f_s$, тут условие выполняется, но равенство получается похожее. В общем, не вижу проблемы "аналитически".

[Евгений Машеров]

Проблема "прагматическая". "Аналитически" тут всё тривиально, следствие из периодичности тригонометрических функций или, как говаривал Козьма Прутков - "желающий обедывать слишком поздно рискует обедывать завтра поутру". А практически - если у нас есть частоты вне полосы, которую мы можем оценивать при данной частоте оцифровки - у нас появляются "призраки",

[Евгений Машеров]

В порядке научного анекдота. Два аспиранта, очень умные и энтузиастические (режим иронии отключён), исследовали электроэнцефалограмму (частотную полосу классически принимают 0.5Гц-35Гц, хотя в последнее время возрос интерес к более высоким частотам, до 70Гц и выше). В сигнале она выделяли кратковременные вспышки на определённых частотах. Разные у разных людей, здоровых испытуемых и больных, но вот две частоты, 22Гц и 28Гц проявлялись почти что у всех больных, при разных патологиях. Чему они пытались найти глубокое объяснение. Но увы. У них частота опроса была 128Гц, что даёт "частоту Найкиста-Котельникова-Шеннона" (никого не забыл? а, ещё Уиттекер) 64 Гц, то есть сетевую наводку (которую отсекает, и успешно, аналоговый режекторный фильтр) они бы увидели, а полоса ЭЭГ заведомо ниже. Только вот аппаратура питается через выпрямитель примерно такой схемы.

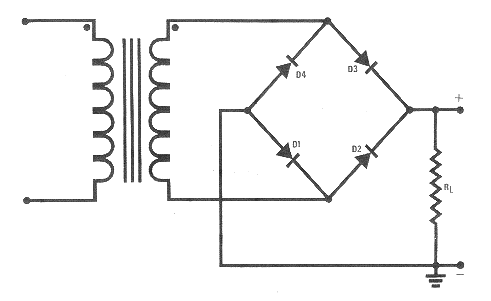
Трансформатор имеет сердечник, который ввиду насыщения порождает кратные нечётные гармоники 150Гц и далее, а диодный мост превращает 50Гц переменного в пульсирующий 100Гц, то есть гармоники чётные, 100Гц и далее.

$150-128=22$

$128-100=28$

А отчего лишь у больных? А их, в отличие от здоровых испытуемых, писали не в экранированной камере в лаборатории, а в палате. Где электроаппаратуры не много, а очень много (особенно в реанимации).
Поэтому на входе ставят аналоговые фильтры (у которых куча недостатков, и малая крутизна среза, и разброс характеристик между каналами, и температурная и не только нестабильность; но они никак не зависят от частоты оцифровки), убирающие частоты выше НКШ с запасом (а уж "филировку" можно и цифровым фильтром сделать), и тем самым избавляющие от "призраков" в смысле алиасов.

[svv]

Kevsh в сообщении #1552867 писал(а):

Допустим, у нас всё плохо и $f_0=0,7f_s$, тогда получаем $\sin(2\pi f_0 k t_s )=\sin(2\pi f_s(0,7 + m)k t_s)$, ну и что ?

Kevsh

svv в сообщении #1552758 писал(а):

Пусть $f_0 \in (0,\frac {f_s}2), \;f=f_s-f_0$, тогда $f\in (\frac {f_s}2, f_s)$.
Покажите, что гармонический сигнал с частотой $f$ неотличим от некоторого гармонического сигнала с частотой $f_0$ по значениям в моменты времени $t=kt_s$.

Покажу на Вашем примере с частотой $0.7f_s$.
Берём в формуле $m=-1$ и получаем:
$\sin(2\pi\cdot 0.7f_s\cdot k t_s )=\sin(2\pi\cdot (0,7 -1)f_s\cdot k t_s)=-\sin(2\pi\cdot 0.3f_s\cdot k t_s)$
То есть гармонический сигнал вида $\sin 2\pi f t$ с частотой $0.7f_s$ неотличим от гармонического сигнала того же вида (только ещё умноженного на $-1$) с частотой $0.3f_s$ по значениям, взятым в моменты времени $kt_s$.

В общем случае гармонический сигнал с частотой $f_0$ неотличим от некоторого гармонического сигнала с частотой $f=f_s-f_0$ по дискретным отсчётам.
Ещё раз повторюсь, что эта неоднозначность несколько иного вида, чем та, о которой говорится в Вашем пособии. Например, "двойником" сигнала с частотой $0.6f_s$ оказывается сигнал с частотой $0.4f_s$.

[Евгений Машеров]

Kevsh в сообщении #1552867 писал(а):

Допустим, у нас всё плохо и $f_0=0,7f_s$, тогда получаем $\sin(2\pi f_0 k t_s )=\sin(2\pi f_s(0,7 + m)k t_s)$, ну и что ? Заменю на $f_0=0,2f_s$, тут условие выполняется, но равенство получается похожее. В общем, не вижу проблемы "аналитически".

Проблема очень простая. В полученном разложении Вы имеете некоторое число, характеризующее $\Sigma_m A_m \sin(2\pi f_s(0,7 + m)k t_s)$. И узнать точное значение коэффициента можете, только если в сумме лишь одно слагаемое. В противном случае у Вас есть сумма коэффициентов, и что с ними делать далее - Вам неведомо.

[svv]

Тут $f_s=t_s=1$. Зелёный сигнал имеет частоту $0.7f_s$, синий $0.3f_s$ и инвертирован. Видно, что по отсчётам, взятым в моменты $kt_s$, их различить нельзя.