Комментарий таков. Если из данных уравнений исключить

, то получится уравнение

к которому применима элементарная версия метода Рунге. Суть ее в том, чтобы составить некоторую дробь

с квадратичными (по

и

) числителем и знаменателем, при этом сама конструкция гарантирует, что значения

будут целыми для любого решения

уравнения

. С другой стороны, отношение

должно оставаться ограниченным для "больших" решений

(т.е. для "далеких" точек кривой

). В результате к исходному уравнению

добавляется еще одно уравнение, которому должны удовлетворять все "большие" решения решения

. Это позволяет найти все "большие" решения уравнения

, просто решив систему из двух алгебраических уравнений. Понятно, что после этого нужно найти и все "маленькие" решения, но это уже можно сделать полным перебором всех кандидатов на роль таковых.
Разумеется, в частных случаях можно отступить от регулярной конструкции дроби

. Например, в данной задаче довольно легко обнаружить, что дробь

должна быть целым числом. В то же время отношение
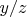
должно быть ограниченным, как следует из уравнения

получаемого из данной системы уравнений исключением

. Это позволяет найти возможные целые значения

и тем самым решить задачу.
В ряде случае вопрос о возможных целочисленных значениях возникающих в элементарной версии метода Рунге дробей

представляет самостоятельный интерес и, более того, может быть решен во всей общности (т.е. без каких бы то ни было ограничений на переменные типа ограниченности их частного). Для дроби

это, увы, не так: легко доказать, что единственным четным целым значением

является ноль, а вот нечетные целые значения

не поддаются простому описанию (их имеется, по-видимому, бесконечно много). Таким образом, здесь приходится апеллировать к ограниченности отношения
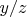
.



