Всем привет!
Вспомнил с универских лет следующую задачку и уже второй день не могу выкинуть из головы

Цитата:
Дана окружность с радиусом
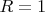
. Окружность вписана в квадрат. Обозначим имеющиеся параметры:
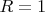
- радиус окружности

- длина окружности

- площадь круга

- периметр квадрата

- площадь квадрата
Затем будет отрезать от квадрата маленькие прямоугольники, которые касаются окружности. Очевидно, что площадь квадрата будет уменьшаться, причем периметр будет сохраняться, т.е.


Если рассмотреть указанные выше последовательности площадей и периметров, то видим, что первая последовательность ограничена снизу площадью круга (т.к. при отрезании мы никогда не "залезаем" на окружность). И к тому же эта последовательность монотонно убывает. По теореме Вейерштрасса из матанализа получаем, что предел последовательности существует. С последовательностью периметров все проще: тут одни константы.
Таким образом, в пределе получим некую фигуру с конкретным значением площади и периметра.
И вот здесь в истории утверждается, что предельная фигура будет являться этой окружностью, т.е.

И как будто бы математики - дураки, число

неверно посчитали

Я понимаю, что подвох в предельном переходе, т.е. фигура, которая получается в пределе не равна окружности. Но с другой стороны, если на шаге

этих "урезаний" провести окружность, которая будет описывать наш "квадрат" таким образом, чтобы она касалась нашего "квадрата", то мы всегда можем еще немного его "подкромсать" со всех сторон, чтобы описать еще более мелкой окружностью, т.е. что-то вроде "для любого эпсилон больше нуля..." можем максимально близко подобраться к окружности. Я веду к тому, что если мы можем максимально близко подводить наш "квадрат" к окружности, то как математически правильно доказать неверность этого утверждения?
Я вдобавок вспомнил, что окружность по сути является последовательностью правильных вписанных многоугольников, и в этом случае последовательность многоугольников действительно сходится к окружности. Может быть, дело в способе "касания" окружности: в случае выше "касание" происходит вершиной, т.е. "острой частью", а в последовательности многоугольников - стороной, т.е. "гладкой частью". Тут дифференцируемость наверно каким-то образом завязана, и в примере выше в пределе получается такой "ежик", который мало где дифференцируем?



