stalvoronЛучше вместо "гравитация" говорить "гравитационное поле" и спрашивать "что такое гравитационное поле"? Вот на этот вопрос есть четкий ответ. Существуют вполне определенные уравнения гравитационного поля. Гравитационное поле - это (в ОТО) метрика пространства-времени.
Метрика - это, можно сказать, масштаб пространства-времени в каждой точке. Например, возьмем глобус и нанесем на него по всей поверхности одинаковые кружки единичного радиуса (слева):
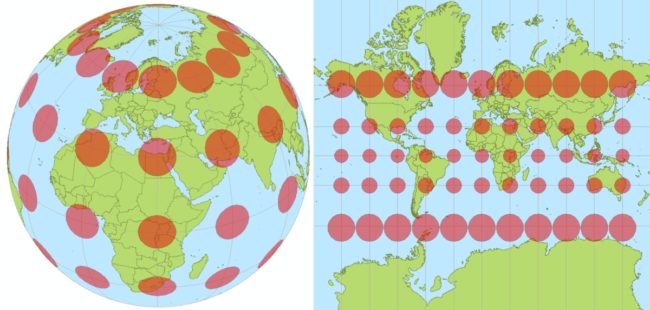
Теперь отобразим поверхность этого глобуса на плоскость (получим карту мира справа). Это одно из бесконечного множества таких отображений сферической поверхности на плоскость. Можете самостоятельно посмотреть другие примеры по поиску "картографические проекции".
Мы видим, что на проекции кружки стали разного размера (появились искажения). Нам бы хотелось получить карту мира без искажений. Важный вопрос: можно ли так отобразить глобус на плоскость, чтобы все кружки, одинаковые на глобусе, были бы одинаковые и на плоскости? Нет, это невозможно. Потому, что сфера искривлена, а плоскость - нет. Именно поэтому проекций глобуса так много. Все они визуально искажают размер или форму кружков тем или иным образом. Эти искажения можно перераспределять по карте туда-сюда, преобразовывать их, но нельзя от них избавится совершенно.
Некоторые проекции (как эта) сохраняют форму (кружки остаются кружками - конформная проекция), но не сохраняют размер. Другие проекции сохраняют площадь, но не сохраняют размер и форму. Третьи - не сохраняют вообще ничего. Например, самая известная проекция выглядит так:
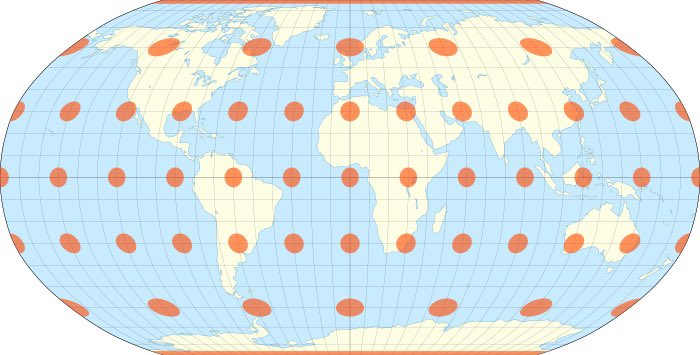
Тут кружки превратились в эллипсы.
Между тем мы точно знаем, что все кружки на глобусе - единичного радиуса. Значит, скажем, на этой карте метр на полюсе выглядит длиннее, чем на экваторе. Более того, метр, не просто выглядит разной длины в разных точках, но он еще и выглядит разной длины по разным направлениям в каждой точке (т.к. кружки стали эллипсами). В каждой точке карты можно нарисовать такой маленький эллипс. Это и есть графическое выражение метрического тензора. Он показывает, как выглядит единичная окружность в каждой точке.
Между прочим, понятие "масштаб карты мира", как видно из этих примеров - это уже тензорная величина. Т.е. нет какого-то одного масштаба на карте мира (в 1 см - 10 000 км). И нет даже своего масштаба в каждой точке карты (в точке с координатами

масштаб равен

). В каждой точке и по каждому направлению - свой масштаб. На самом деле это не совсем произвольно, конечно. Иначе в каждой точке получились бы произвольные кляксы, а не эллипсы. Поэтому масштаб - это все же тензор, а не произвольная функция

.
Для трехмерного пространства это были бы эллипсоиды, а для четырехмерного пространства-времени это четырехмерные гиперболоиды (к сожалению, там несколько сложнее получается).
Но суть все равно не меняется. Искривленное пространство - это пространство, у которого в каждой точке задана метрическая фигура (эллипс в данном случае), которая показывает, как выглядит в данной точке единичная окружность. Задать такие фигуры во всех точках - значит задать метрику. Эти эллипсы и есть графическое выражение гравитационного поля.
Разумеется, это только аналогия. Пространство-время не поддается такой простой визуализации потому, что оно четырехмерно, а так же потому, что оно псевдоевклидово. Но тем не менее основная идея верная. В пространстве-времени тоже можно нарисовать такие фигуры (световые конусы и вписанные в них гиперболоиды) в каждой точке.
Это мы сейчас только приблизительно представили, что такое гравитационное поле в ОТО. У Ньютона это было всего-лишь одно число в каждой точке пространства (гравитационный потенциал). В ОТО это четырехмерный "метрический эллипсоид" в каждой точке пространства-времени, который описывается десятью параметрами.
А ведь теперь еще нужно понять, как материя влияет на вид этих "эллипсоидов", т.е. как создается это гравитационное поле? У Ньютона это было очень просто: в каждой точке пространства было одно число (плотность массы), которое очень просто создавало гравитационный потенциал. В ОТО за это отвечает другой тензор - тензор энергии-импульса. Мы уже видели, что тензор гораздо сложнее числа. В тензор энергии-импульса кроме плотности массы (или энергии, что одно и то же) входит, помимо прочего, еще и трехмерный тензор напряженного состояния материи (давление). Это нечто совершенно новое в сравнении с тяготением Ньютона. Давление дает вклад в гравитационное поле. Поэтому чем массивнее тело, тем больше давление в его недрах, тем сильнее это давление влияет на метрику пространства-времени, а это приводит к последующему изменению давления. Скажем, оно может усиливаться.