Наилучшее место для замены карабина на ролик в полиспасте

[someniatko]

Продолжая (точнее, уже заканчивая) проходить школьные темы по физике за 7 класс, наткнулся на неожиданное для меня явление.

Имеется полиспаст для альпинистов, скажем 6:1 или 7:1, составленный из нескольких верёвок, а вместо блоков используются карабины. Естественно этот факт сильно увеличивает роль силы трения верёвки о блок (а точнее карабин), и её уже нельзя игнорировать как в типовых школьных задачах. Допустим теперь, что у нас в распоряжении есть один ролик, который мы можем использовать в полиспасте вместо карабина, чтобы сильно уменьшить силу трения. Мы конечно же хотим разместить ролик в самом эффективном месте, чтобы максимизировать КПД всего полиспаста.

Примеры схем таких полиспастов (взял отсюда):


Согласно закону Амонтона — Кулона, а это единственное на что я могу опираться на данный момент, $F = \mu N$, где N — сила реакции опоры, т.е. нашего карабина на верёвку. По моим представлениям, возможно неверным, эта сила должна быть как-то пропорциональна силе натяжения верёвки, что проходит через карабин. Сила натяжения верёвки максимальна у той, что возле крепления груза, и минимальна у свободной верёвки, за которую предполагается тянуть. Поэтому я предположил, что разумно заменить на ролик именно тот карабин, который ближайший к грузу.

Но многочисленные источники, в том числе это видео на ютуб говорят обратное, мол напротив в первую очередь нужно менять ближайший к рукам альпиниста карабин, а не ближайший к грузу. Более того, в видео это доказано и на опыте. Я конечно попытался для себя это объяснить, но пока безрезультатно. Вот мои мысли: полиспаст, позволяя нам выиграть в силе, при этом заставляет нас тянуть большую длину верёвки. Соответственно, длина верёвки, которая пройдёт через ближайший к нашим рукам блок (карабин / ролик) больше, чем та, что пройдёт через ближайший к грузу, а значит скорость прохождения верёвки больше. Но по закону Амонтона — Кулона сила трения никак не зависит от скорости относительного движения тел (верёвки и блока), а значит этот фактор по идее не должен оказывать влияния. Влияет ли скорость прохождения на силу реакции опоры, или здесь закон $F = \mu N$ просто неприменим?

Заранее спасибо за ответ на глупый вопрос :)
UPD: исправил таймкод в ссылке на видео

[EUgeneUS]

someniatko в сообщении #1545153 писал(а):

Но многочисленные источники, в том числе это видео на ютуб
говорят обратное, мол напротив в первую очередь нужно менять ближайший к рукам альпиниста карабин, а не ближайший к грузу.

Посмотрел этот познавательный ролик целиком, но такой рекомендации не услышал
Дайте, пожалуйста, точный тайминг, где звучит такая рекомендация.

Расчет простой.
Пусть при обходе ролика или карабина сила натяжения веревки уменьшается с коэффициентом $k$ (то есть, если до ролика\карабина сила была $T$, то после будет $kT$).
Пронумеруем ролики\карабины.
После чего аккуратно, с учетом обхода каждого ролика рассчитаем силу натяжения веревки на каждом участке.
После чего суммируем то, что приходит на груз и получим силу на грузе с учетом потерь на роликах\карабинах.
И посмотрим, где "плохой" ролик (он же карабин), с маленьким $k$ будет вносить наименьшие потери в суммарную силу.
Или где замена карабина на хороший ролик даст наибольший выигрыш в силе на грузе.

Я это сделал для простого полиспаста 4:1 и для сложного полиспаста 6:1. Для простого полиспаста, на ролик нужно менять карабин наиболее близкий к альпинисту.
То есть вывод прямо противоположный, чем у Вас.
Для сложных полиспастов чуть интереснее получается, наиболее выгодный может оказаться ролик и не самый близкий к альпинисту. Но в любом случае - не самый близкий к грузу.

-- 05.01.2022, 03:50 --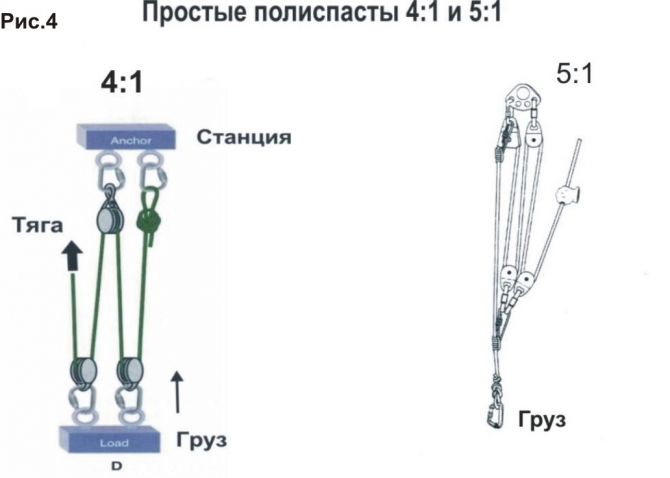



Пример расчета для простого полиспаста 4:1.
Нумерация ветвей и роликов слева направо.
Тянем с силой $T$ (натяжение первой ветви)
После прохода первого ролика сила натяжения веревки $k_1T$
После прохода второго ролика сила натяжения веревки $k_1 k_2 T$
После прохода второго ролика сила натяжения веревки $k_1 k_2 k_3 T$
Все эти силы приложены к грузу, тогда сила на грузе:
$F = T (1 + k_1 + k_1 k_2 + k_1 k_2 k_3)$

Легко видеть, что если у нас два ролика с $k < 1$ и один ролик с $k =1$, то максимальная сила на грузе будет, если хороший ролик будет первым (в этом примере, первый ролик закреплен на грузе, но он же является ближайшим к альпинисту).

[sergey zhukov]

someniatko
Кстати, в простом палиспасте сила натяжения веревки максимальна именно там, где тянет человек. По мере прохождения через ролики и карабины к грузу сила натяжения все время падает. Так что по крайней мере для простого полиспаста все достаточно ясно: ролик нужно ставить ближе в тому, кто тянет.

В этом видео вначале было показано, что простой полиспаст с отношением более 4:1, собранный на карабинах, уже не дает вообще никакого выиграша в силе (и даже делает подьем еще труднее).
Между тем можно рассмотреть эту задачу даже и с бесконечным количеством одинаковых карабинов в простом полиспасте. Пусть человек тянет с усилием $F$, причем после первого карабина натяжение веревки падает до $kF$ ($k<1$), после второго - $k^2F$, после третьего - $k^3F$ и т.д. Это соответствует идеализированным представлениям о трении веревки о карабин. Тогда, если число роликов бесконечно, таким полиспастом можно поднять груз весом $T=\frac{F}{1-k}$. Если $k=1$, то ролики идеальны и $T \to \infty$. Если же они не идеальны, то все равно такой полиспаст дает большой выигрыш в силе.

Это показывает, что трение в реальных карабинах растет быстрее натяжения веревки.

[someniatko]

EUgeneUS в сообщении #1545167 писал(а):

$F = T (1 + k_1 + k_1 k_2 + k_1 k_2 k_3)$

Легко видеть, что если у нас два ролика с $k < 1$ и один ролик с $k =1$, то максимальная сила на грузе будет, если хороший ролик будет первым (в этом примере, первый ролик закреплен на грузе, но он же является ближайшим к альпинисту).

Большое спасибо! Расчёт действительно оказался простым, и первый коэффициент сопротивления $k_1$ влияет на потерю силы в каждом последующем карабине. Посыпаю голову пеплом что не догадался, что сила натяжения верёвки будет постепенно падать, последовательно проходя через карабины, и исходя из этого нужно было аккуратно составить формулу силы, действующей на груз.

EUgeneUS в сообщении #1545167 писал(а):

Дайте, пожалуйста, точный тайминг, где звучит такая рекомендация.

Начало опыта: https://www.youtube.com/watch?v=SKd-YzfaJ3Q&t=1165s 19:25
Вывод и рекомендация ("третье правило полиспаста"): https://www.youtube.com/watch?v=SKd-YzfaJ3Q&t=1266 21:06