Термех.Динамика

[ysergich]

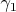
Однородный конус высотой H и плотностью $\gamma_1$ погружен в жидкость плотности $\gamma_2 (\gamma_2>\gamma_1)$, так что его вершина находится на поверхностью жидкости, а основание параллельно этой поверхности. Определить период собственных вертикальных колебаний конуса, пренебрегая сопротивлением жидкости.
Обозначаю погруженную часть как $V_1$ (усеченный конус) с высотой $h$. Смещение за $x$, изменение высоты при *всплывании* конуса h-x.
Равновесие:
$mg=\gamma_2gV_1, V_1=\frac {1}{3}\Pih(R^2+Rr+r^2)$
Далее переходим к динамике:
$mx''=mg-\gamma_2gV_2, V_2=\frac {1}{3}\pi(h-x)(R^2+Rr_1+r_1^2)$
Что делать дальше не знаю, пытался найти $x$ и подставить начальные условия t=0, x'=0, то получается какая то фигня. Пробовал выражать радиусы через тангенс угла у вершины, только толку ноль. Прошу направить в правильное русло, буду премного благодарен.

[Gagarin1968]

ysergich в сообщении #1541041 писал(а):

Обозначаю погруженную часть как $V_1$ (усеченный конус) с высотой $h$.

Как может быть погружён усечённый конус, если перед этим Вы пишете, что вершина конуса находится на поверхности жидкости?
P.S. Ой, только сейчас обратил внимание, что Вы дублируете вот эту тему из Карантина. А это по Правилам нельзя. Лучше исправляйте там, а то модератор будет недоволен. И заодно исправьте формулировку задачи.

[ysergich]

Gagarin1968 в сообщении #1541046 писал(а):

ysergich в сообщении #1541041 писал(а):

Обозначаю погруженную часть как $V_1$ (усеченный конус) с высотой $h$.

Как может быть погружён усечённый конус, если перед этим Вы пишете, что вершина конуса находится на поверхности жидкости?
P.S. Ой, только сейчас обратил внимание, что Вы дублируете вот эту тему из Карантина. А это по Правилам нельзя. Лучше исправляйте там, а то модератор будет недоволен. И заодно исправьте формулировку задачи.

Часть конуса погружена в воду, поэтому я разделил погружённую и находящуюся над водой части.Рассматривал их отдельно.Как вы видите решение данной задачи?

[мат-ламер]

ysergich
Мне кажется, что вы уравнение неправильно составили. Если

ysergich в сообщении #1541041 писал(а):

Смещение за $x$,

- малое смещение конуса, то уравнение относительно его должно иметь вид: $x''=\alpha x$ , где $\alpha$ - некая отрицательная константа. У вас же уравнение имеет вид: $x''=\alpha (h-x)$ .

[ysergich]

мат-ламер в сообщении #1541056 писал(а):

ysergich
Мне кажется, что вы уравнение неправильно составили. Если

ysergich в сообщении #1541041 писал(а):

Смещение за $x$,

- малое смещение конуса, то уравнение относительно его должно иметь вид: $x''=\alpha x$ , где $\alpha$ - некая отрицательная константа. У вас же уравнение имеет вид: $x''=\alpha (h-x)$ .

Помогите составить уравнение правильно

[мат-ламер]

ysergich в сообщении #1541057 писал(а):

Помогите составить уравнение правильно

Возможно "неправильно" - не то слово (может я не разобрался в ваших обозначениях). Просто желательно привести уравнение к тому виду, что я написал. Для него период колебания уже легко находится. Попробуйте сами для начала продолжить.

-- Вт ноя 30, 2021 11:30:48 --

ysergich в сообщении #1541041 писал(а):

Прошу направить в правильное русло,

ysergich в сообщении #1541057 писал(а):

Помогите составить уравнение правильно

Так направить в русло или решить за вас?

[Pphantom]

ysergich, замечание за дублирование темы из Карантина. Исправляйте ее, эта тема закрыта и будет удалена.